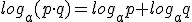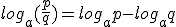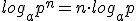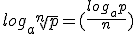1.2. Aprendemos a multiplicar

Como todo en las matemáticas, los logartimos se descubren por necesidades de la humanidad. En este caso la necesidad de realizar grandes operaciones aritméticas, en concreto multiplicaciones y divisiones. Gracias a los logartimos, las enormes multiplicaciones relacionadas con distancias espaciales se podían convertir en sumas, utilizando una serie de propiedades. Las famosas tablan de logaritmos ayudanban a realizar estas transformaciones. En este video conoceras a Vicente Vázquez Queipo, matemático español que se hizo muy famoso debido a la elaboración de las tablas de logaritmos desde el 1 hasta el 2000.

 


 

 



 

Actividad

 Propiedades

 

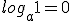Estas propiedades son muy fáciles de recordar, tan solo debes pensar en la definición de logaritmos. Veamos la primera propiedad 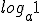   ¿Cuál es el exponente al que debemos elevar a un número para que el resultado sea 0? Recuerda las propiedades de los número exponenciales. Cualquier número elevado a 0 es 1, por lo que  . Puedes razonar igual con el resto de las propiedades.

Pregunta de Elección Múltiple

Pregunta

Calcula

Respuestas

-1

0

1

2

Retroalimentación

Pregunta

Determina

Respuestas

-5

0

1

5

Retroalimentación

Actividad

 Operaciones

El logaritmo de un producto es la suma de los logaritmos

El logaritmo de uncociente es la diferencia  de los logaritmos

El logaritmo de una potencia es el exponente multiplicado por el logaritmo de la base

El logaritmo de una raíz es el logaritmo del radicando dividido por el índice

Pregunta Verdadero-Falso

Antonio es un alumno de 4.º de ESO que en su examen de logaritmos ha obtenido 4.5. En una de las preguntas, Antonio ha indicado lo siguiente log (7+5) = log 7 + log 5 y su profesor  lo ha tachado. Antonio está convencido que el ejercicios es correcto y que superará el examen. ¿Puedes indicar si el razonamiento de Antonio es correcto?

Pregunta 1

El razonamiento de Antonio es correcto.

Sugerencia

Observa las propiedades de los logaritmos.

Caso de estudio

Si sabemos que  log 2 ≈ 0.3  y log 3 ≈ 0.48, calcula los siguientes valores:


Imagen propia bajo CC
  1. log 20
  2. log 60
  3. log 0.3
  4. log 45

 

Utiliza las propiedades vistas en el anterior "Importante". Ten en cuenta siempre que conoces los valores de log 10 y de las potencias de 10, log 10 = 1, log 100 = 2

Importante

No olvides que a la hora de calcular logaritmos siempre tienes que tener en cuenta la base aplicada.

Por ejemplo, si trabajas con logaritmos en base 3 (log3), sabes que log3 3 = 1 , log3 9 = 2 o que log3 27 = 3.

Caso de estudio

Si sabemos que  log 2 ≈ 0.3  y log 3 ≈ 0.48, calcula el valor de log 2.88.