Resumen
Importante
Si tenemos una función f(x) denominamos función derivada de f respecto a la variable x a una nueva función que para cada valor x nos proporciona la derivada de la función en el punto x. A la función derivada de f(x) la denotaremos f'(x), aunque también la puedes ver representada como ![]() . De esta forma tenemos que:
. De esta forma tenemos que:
![]()
Recuerda que con esta definición, la función derivada nos proporciona, para cada punto x, la pendiente de la recta tangente a la función en en punto x.
Importante
Es conveniente aprenderse esta tabla para no tener que recurrir una y otra vez a la definición cada vez que necesitemos derivar una función.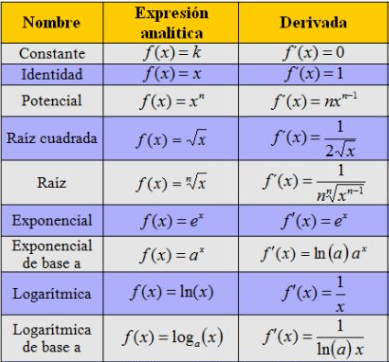
Importante
| Suma | (f+g)'=f'+g' |
La derivada de la suma de funciones es la suma de las derivadas de estas funciones |
| Resta | (f-g)'=f'-g' |
La derivada de la diferencia de funciones es la diferencia de las derivadas de estas funciones |
| Producto |
(f·g)'=f'·g+g'·f |
La derivada del producto de dos funciones es igual a la derivada de la primera por la segunda sin derivar más la segunda derivada por la primera sin derivar. |
| Cociente |
La derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador sin derivar menos la derivada del denominador por el numerador sin derivar, y todo ello dividido por el denominador al cuadrado |
|
| Producto por un número | (a·f)'=a·f' |
La derivada del producto de un número real por la función es igual al número real por la derivada de la función |
| Composición |
(g°f)'=[g(f(x))]'=g'(f(x))·f'(x) |
Regla de la cadena |
| RESUMEN | Vídeo 1 | |
| EJERCICIOS | Vídeo 1 |