3. Reglas de derivación
Importante
| Suma | (f+g)'=f'+g' |
La derivada de la suma de funciones es la suma de las derivadas de estas funciones |
| Resta | (f-g)'=f'-g' |
La derivada de la diferencia de funciones es la diferencia de las derivadas de estas funciones |
| Producto |
(f·g)'=f'·g+g'·f |
La derivada del producto de dos funciones es igual a la derivada de la primera por la segunda sin derivar más la segunda derivada por la primera sin derivar. |
| Cociente |
La derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador sin derivar menos la derivada del denominador por el numerador sin derivar, y todo ello dividido por el denominador al cuadrado |
|
| Producto por un número | (a·f)'=a·f' |
La derivada del producto de un número real por la función es igual al número real por la derivada de la función |
| Composición |
(g°f)'=[g(f(x))]'=g'(f(x))·f'(x) |
Regla de la cadena |
| RESUMEN | Vídeo 1 | |
| EJERCICIOS | Vídeo 1 |
Veamos unos ejemplos mas en la siguiente presentación
La mejor forma de aprender a derivar es derivando, así que aquí tienes unos videos del Profesor de la Universidad Politécnica de Cartagena Juan Medina Molina (lasmatematicas.es). Quizás sea una buena idea que pinches para verlos en pantalla completa, o pinchando sobre ellos para verlos en la página de youtube:
| Derivada de un monomio |
Derivada de una exponencial | Derivada de un polinomio |
Derivada de un producto |
| Derivada de un cociente | Derivada de una composición |
||
Para saber más
Aunque te hemos proporcionado reglas de derivación para funciones elementales sencillas existen reglas para muchas otras funciones. En este documento puedes encontrar una completa tabla de derivadas que nos proporciona la web 3con14. Pulsa sobre la imagen para verla ampliada.
Ejercicio Resuelto
|
Para practicar Para practicar el cálculo de derivadas te proporcionamos una relación de ejercicios resueltos de la web 3con14. Coge lápiz y papel e intenta obtener la derivada sin mirar las soluciones. Comprobarás que con la práctica irás cogiendo más soltura en el cálculo de derivadas. Pulsa sobre la imagen para ver el documento. |
Caso práctico
Dada la función
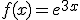 |
- Calcula la ecuación de la recta tangente en x=0.
Caso práctico
Conocimiento previo
Si este tema ha despertado tu curiosidad y quieres seguir indagando, te recomendamos la serie documental "Universo matemático" de rtve que recorre la historia de las matemáticas, desde los pitagóricos hasta los investigadores del presente. Su objetivo es enseñar como la aparición de nuevas ideas matemáticas responde a los problemas concretos de cada época y contexto.
En concreto el programa "Sobre hombros de gigantes; Newton y Leibnitz", no habla sobre los dos científicos que a mediados del siglo XVII revolucionan la historia de la ciencia, Newton y Leibnitz. Ambos en el campo del cálculo diferencial.
Para saber más
Si este tema ha despertado tu curiosidad y quieres seguir indagando, te recomendamos la serie documental "Universo matemático" de rtve que recorre la historia de las matemáticas, desde los pitagóricos hasta los investigadores del presente. Su objetivo es enseñar como la aparición de nuevas ideas matemáticas responde a los problemas concretos de cada época y contexto.
En concreto el programa "Sobre hombros de gigantes; Newton y Leibnitz", no habla sobre los dos científicos que a mediados del siglo XVII revolucionan la historia de la ciencia, Newton y Leibnitz. Ambos en el campo del cálculo diferencial.