2.2. Integración por partes
 |
| Colaboradores Imagen obtenida del banco de imágenes del ITE |
En algunas ocasiones encontramos integrales que no son inmediatas y para las que el método de sustitución que hemos tratado anteriormente tampoco funciona. En estas ocasiones podemos intentar utilizar otro método llamado por partes. ¿Cómo se utiliza este método? te explicamos un poco
Importante
Si tenemos dos funciones 
y 
, y 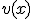consideramos la función que resulta de multiplicar las dos anteriores 
entonces, de la derivada de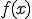 
es: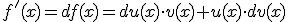 
Si calculamos la integral a ambos lados de la igualdad tenemos que:
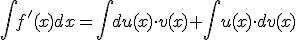
Es decir: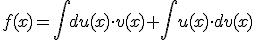 
Luego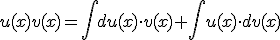 
Por tanto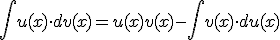 
En el siguiente vídeo puedes ver cómo podemos aplicar esta fórmula:
En la siguiente presentación PDF puedes observar este método resumido y aplicado:
Ejemplo o ejercicio resuelto
Calcula las siguientes integrales en las que intervienen funciones trigonométricas
a) 
b) 
Ejemplo o ejercicio resuelto
 |
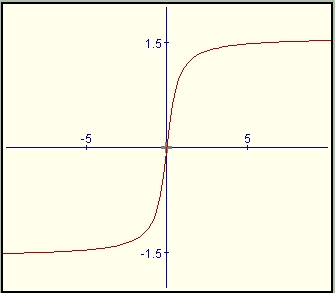En la imagen de la derecha observamos la gráfica de la función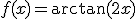 
que vemos que se anula en 
.
Si 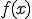es la función derivada de la función 
, sabemos que tiene un máximo, un mínimo o un punto de inflexión en el punto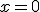 
.
Si sabemos que 
, calcula la función
AV - Reflexión
Resuelve por partes la siguiente integral: 
AV - Actividad de Espacios en Blanco
Escribe al lado de cada integral la letra cuya solución que le corresponde sabiendo que
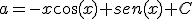
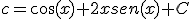
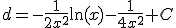
Puedes ver un resumen de este método en el siguiente vídeo:
Vídeo de universidadurjc alojado en Youtube
Para saber más
 |
Para seguir investigando sobre la utilización del método de integración por partes, te aconsejamos que visites el siguiente enlace.