1. La integral indefinida. Primitiva de una función
Ya sabemos del tema anterior que integrar es el proceso contrario o recíproco a derivar. Es decir, dada una función f(x) se trata de buscar todas las funciones F(x), llamadas primitivas de f, tales que, al derivarlas, obtenemos f(x). También sabemos ya que todas las primitivas de una función se diferencian en una constante, por tanto, si la función se puede integrar, existen infinitas primitivas de la misma.
Definiremos la integral indefinida de f(x) como el conjunto de las infinitas funciones primitivas que puede tener, diferenciándose todas ellas en una constante.
La pregunta que nos hacemos ahora es: si conocemos la función derivada de otra, ¿podemos conocer la función de la que es derivada?. En algunos casos es bastante sencillo de resolver, pero en otros no.
Puedes ver en la siguiente escena de Geogebra las primitivas de las funciones del tipo xn, variando tú mismo el valor de n en la barra deslizadora. También puedes ver sus infinitas primitivas variando el valor de la constante c.
Escena de Nury Andrea Rodríguez Pardo alojada en Geogebra. Licencia CC
Importante
Si tenemos una función f(x) llamamos primitiva de f(x) respecto a la variable x a una función F(x) que cumple que:
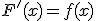
Si F(x) es una primitiva cualquiera de f(x), entonces F(x) + C también será una primitiva de f(x), siendo C un número real cualquiera.
Llamamos integral indefinida de f(x) al conjunto de las infinitas primitivas que tiene f(x), que vendrán dadas por F(x) + C.
Se representa de la siguiente forma:
![]()
donde
![]() denota el símbolo de integración,
denota el símbolo de integración,
f(x) es el integrando o función a integrar y
dx es el diferencial de x que indica la variable con respecto a la que se está integrando
C es un número real cualquiera.