2.1. Ecuación vectorial y paramétrica del plano
Importante
Para obtener la ecuación de una recta, que tiene dimensión 1, ya has visto que necesitábamos de un punto y un vector director. Ahora, para obtener la ecuación de un plano, vamos a necesitar de un punto 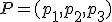 y dos vectores directores
y dos vectores directores 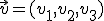 y
y 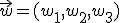 , que deben ser linealmente independientes, y los puntos del plano serán aquellos que se obtengan de sumarle al punto una combinación lineal de los dos vectores directores. Así, la ecuación vectorial del plano
, que deben ser linealmente independientes, y los puntos del plano serán aquellos que se obtengan de sumarle al punto una combinación lineal de los dos vectores directores. Así, la ecuación vectorial del plano 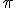 es:
es:
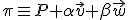
Desarrollándola: 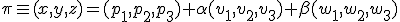
Ejemplo o ejercicio resuelto
 |
| Torre Eiffel Imagen del ITE. |
Un diseñador quiere hacer un corte transversal de la torre Eiffel para hacer un cartel con una vista innovadora de esa torre.
Para ello quiere que el corte pase por los puntos 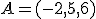 ,
, 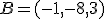 y
y 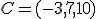 . Calcula la ecuación vectorial del plano de corte.
. Calcula la ecuación vectorial del plano de corte.
AV - Pregunta Verdadero-Falso
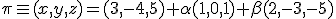
Retroalimentación
Verdadero
Retroalimentación
Verdadero
Cierto, basta hacer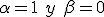
Retroalimentación
Falso
No, es un vector dirección del plano.Retroalimentación
Verdadero
Importante
Dado un punto 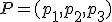 y dos vectores
y dos vectores 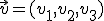 y
y 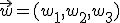 sabemos que la ecución vectorial del plano que pasa por el punto y tiene esos dos vectores directores es
sabemos que la ecución vectorial del plano que pasa por el punto y tiene esos dos vectores directores es
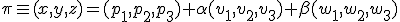
Igualando coordenada a coordenada tenemos que:
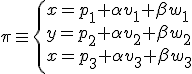
A esta ecuación se le llama ecuación paramétrica del plano. En la siguiente imagen interactiva puedes ver como se obtienen los puntos del plano a través de uno de sus puntos y la combinación lineal de sus vectores directores.
Ejemplo o ejercicio resuelto
Calcula la ecuación paramétrica del plano que pasa por el punto 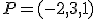 y tienen por vectores directores los vectores
y tienen por vectores directores los vectores 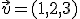 y
y 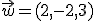 . Calcula otro punto del plano
. Calcula otro punto del plano
Ejemplo o ejercicio resuelto
Dado el plano 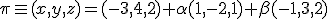 Calcula la ecuación paramétrica del plano paralelo al anterior y que pase por el punto
Calcula la ecuación paramétrica del plano paralelo al anterior y que pase por el punto 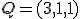 .
.