1.2. Ecuación paramétrica y continua de la recta
Curiosidad
En el siguiente vídeo puedes ver una curiosa historia que se desarrolla entre una línea y un punto
Importante
Así, dado un punto 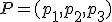 y un vector
y un vector 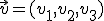 hemos visto que la ecuación vectorial de la recta se obtiene como
hemos visto que la ecuación vectorial de la recta se obtiene como

Si desarrollamos la ecuación tenemos que

Y para que esta igualdad se verifique se debe cumplir que
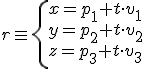
Esta última ecuación se llama ecuación paramétrica de la recta. Para obtener esta ecuación observamos que basta con tener un punto de la recta y un vector director.
Ejemplo o ejercicio resuelto
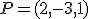 y tiene como vector director
y tiene como vector director 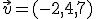 . Calcula también otro punto de esta recta.
. Calcula también otro punto de esta recta.
Ejemplo o ejercicio resuelto
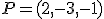 y
y 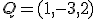 . Represéntala en la escena que encuentras más abajo y calcula otro punto
. Represéntala en la escena que encuentras más abajo y calcula otro punto 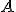 de esta recta. Dibuja más abajo la recta que pasa por
de esta recta. Dibuja más abajo la recta que pasa por 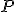 y por
y por 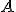 y observa que es la misma que la primera.
y observa que es la misma que la primera.
AV - Actividad de Espacios en Blanco
Dadas las siguientes rectas
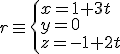
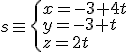

Importante
Seguimos profundizando en la ecuación de la recta. Sabemos que para obtener la ecuación de una recta necesitamos un punto 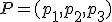 y un vector director
y un vector director 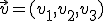 . A partir de estos datos ya sabemos cómo obtener dos ecuaciones distintas de la misma recta. La ecuación vectorial:
. A partir de estos datos ya sabemos cómo obtener dos ecuaciones distintas de la misma recta. La ecuación vectorial:

y la ecuación paramétrica:
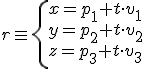
A partir de la ecuación paramétrica, depejando el parámetro 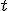 en cada ecuación tenemos que:
en cada ecuación tenemos que:
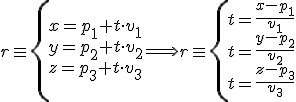 Por tanto
Por tanto
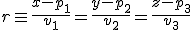
A esta ecuación se le llama Ecuación continua de la recta.
Ejemplo o ejercicio resuelto
 |
|
Teléfono. |
Un ingeniero ha diseñado los planos de un edificio y sabe que el cable de teléfono del mismo, que baja en línea recta, pasa por los puntos 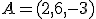 y
y 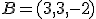 . El problema es que debe atravesar alguno de los muros de carga del edificio que, según el diseño, son puntos en el que alguna de las coordenadas es nula. Calcula la ecuación continua de la recta que sigue el cable y calcula los puntos en los que puede haber algún problema. Dibuja la recta en la escena interactiva que aparece más abajo.
. El problema es que debe atravesar alguno de los muros de carga del edificio que, según el diseño, son puntos en el que alguna de las coordenadas es nula. Calcula la ecuación continua de la recta que sigue el cable y calcula los puntos en los que puede haber algún problema. Dibuja la recta en la escena interactiva que aparece más abajo.
Ejemplo o ejercicio resuelto
Calcula la ecuación continua de la recta que pasa por el punto 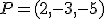 y es paralela a la recta de ecuación
y es paralela a la recta de ecuación
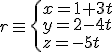
AV - Pregunta Verdadero-Falso
Dada la recta 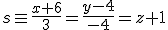
Retroalimentación
Falso
Retroalimentación
Falso
Retroalimentación
Verdadero
Retroalimentación
Verdadero
Retroalimentación
Falso
Retroalimentación
Verdadero
Retroalimentación
Verdadero