2. Estructura cristalina
Actividad
La materia cristalina se caracteriza por poseer las siguientes propiedades: periodicidad, homogeneidad, anisotropía y simetría.
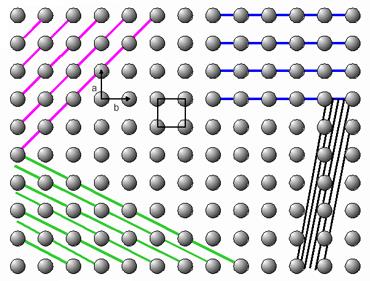 |
| Periodicidad de la materia cristalina. Imagen del ITE en Proyecto Biosfera. Licencia cc
|
- Periodicidad: es la propiedad más característica e importante del estado sólido cristalino, y consiste en la repetición de sus componentes en el espacio siguiendo unas pautas que generan orden. La periodicidad es la causa de la existencia de redes cristalinas.
- Homogeneidad: los cristales tienen -teóricamente- la misma composición química en toda su extensión, por lo que esta puede expresarse con una fórmula química. Los cristales reales (los minerales, por ejemplo), tienen impurezas o pequeñas variaciones composicionales, que hacen variar algunas de sus propiedades.
- Anisotropía: las distancias entre nudos o puntos y las propiedades, varían según las direcciones del espacio que se consideren. En realidad, existe un medio cristalino -el del sistema cúbico- que es isótropo por ser isométrico; es decir sus átomos o iones se encuentran repartidos a intervalos fijos en las tres direcciones del espacio.
- Simetría: es la propiedad por la que se hacen coincidir puntos o elementos del cristal al generar movimientos de traslación, inversión, giro y reflexión a partir de operadores geométricos (centro, ejes y planos).
Objetivos
|
|
|
Difracción de Rayos X |
El estudio de los minerales estuvo ligado en los siglos XVIII a XIX al reconocimiento de la morfología y propiedades observables a simple vista. Se pensaba que el interior de los minerales estaba ocupado por pequeños volúmenes que repitiéndose llenaban el espacio y originaban la forma externa, que fue lo que más llamó la atención al principio.
A comienzos del S. XX, el físico alemán Max von Laüe y colaboradores, descubrieron la ordenación interna de la estructura real de los cristales cuando intentaban demostrar la naturaleza ondulatoria de la radiación X. En la experiencia proyectaron haces de rayos X sobre cristales, recogiendo la radiación resultante en una placa fotográfica. La radiación atravesaba el cristal sin interferir con ningún átomo, llegando a impresionar la pantalla. Se difractaba cuando en su trayectoria interfería con átomos.
Se demostró que los rayos X tenían naturaleza ondulatoria y que sus longitudes de onda estaban próximas a la distancia entre puntos o planos materiales del cristal. Las figuras que se proyectaban en las placas recibieron el nombre de laüegramas. Se comprobó que cumplían leyes geométricas propias para cada tipo de sustancia; por lo que caracterizaban el “secreto” de cada cristal: la estructura ordenada interna de sus átomos.
Puedes aprender más sobre la difracción de rayos X en esta página de cristalografía, o en esta.
 |
 |
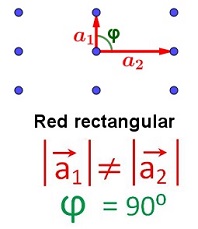
| Ejemplo de red plana Imagen de elaboración propia |
Celda unidad Imagen de Martín Martínez-Ripolls en Crystallography. Licencia cc |
Una sucesión de puntos que se repiten en una misma dirección a intervalos fijos (traslaciones) constituye una fila reticular. Cuando los nudos o puntos reticulares se repiten a lo largo de dos direcciones del espacio, forman un plano reticular o red plana, que queda definida por los valores de dos traslaciones y el ángulo que éstas forman entre sí. Existen 5 redes planas posibles: hexagonal, rectangular centrada o rómbica, oblicua o romboédrica, rectangular y cuadrada.
La superposición de redes planas origina repeticiones de nudos o puntos reticulares manteniendo constantes tres traslaciones unitarias en tres direcciones del espacio. Así se forma red espacial, cuyo menor volumen posible recibe el nombre de celda unidad, definida por 3 traslaciones (a, b, c) y los 3 ángulos (α, β, γ) comprendidos entre las direcciones que marcan las traslaciones o los ejes cristalográficos (x, y, z).
En el S.XIX, Bravais dedujo la existencia de 14 redes espaciales posibles, superponiendo redes planas y estudiando la compatibilidad con la simetría que necesariamente había de tener. En este enlace puedes ver las 14 redes de Bravais , sus celdillas y los sistemas a los que pertenecen.
El desarrollo de la teoría reticular se llevó a cabo paralelamente al estudio de la geometría y simetría de los cristales. Y aunque el estudio teórico de las redes perdió interés para los científicos, recientemente ha vuelto a cobrar importancia en los estudios de física del estado sólido y en el análisis de sustancias cristalinas en base a la difracción de rayos X.
Actividad
Para entender el orden interno de los cristales hay que considerar tres cosas:
1. Nudo (motivo): cualquier átomo, ion o molécula que se repita en la estructura tridimensional del cristal.
2. Traslación: operación por la cual un nudo se repite a una distancia constante del anterior (a, b, c).
3. Ángulo (α,β,γ): ángulo que forman los ejes reticulares entre si.
La red cristalográfica está formada por el conjunto de elementos que se repiten en ciertas direcciones manteniendo constantes unas distancias y unos ángulos.
Rellenar huecos
Relaciona las palabras de las dos filas indicando en cada casilla el número correspondiente.
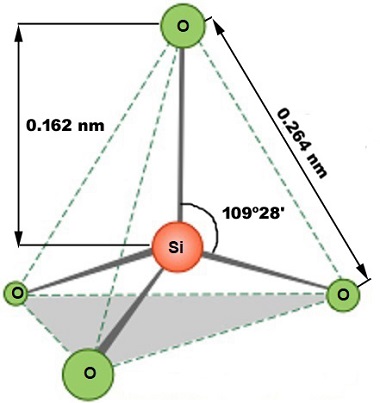 |
| Tetraedro de silicio Imagen adaptada de chemwiki.ucdavis.edu en Socratic.org. Licencia cc |
Por otra parte, el estudio de las redes se puede abordar también considerando que los nudos o puntos reticulares son átomos, iones o moléculas concretos. El caso más simple y frecuente es el de los edificios iónicos, en el que cada ión ocupa un punto de la red con su radio y su carga eléctrica, quedando rodeado siempre de un número fijo de otros de carga opuesta, que se llama número de coordinación. Los más frecuentes son 4, 6, 8 y 12, dependiendo de la relación o cociente entre el radio del catión y el del anión.
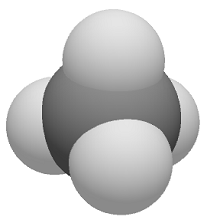
Las figuras geométricas resultantes al rodear cada ion por otros de signo contrario se llaman poliedros de coordinación o redes químico‑estructurales, como: el tetraedro, octaedro, cubo y la combinación cubo-octaedro, etc. Un caso concreto sería la unidad elemental de los silicatos: el tetraedro formado por cuatro átomos de oxígeno y uno de silicio.
|
|
|
|
|
Número de coordinación 4 |
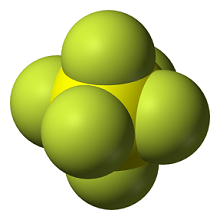
Número de coordinación 6 |
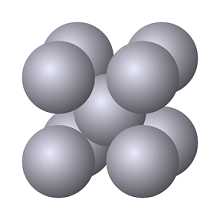
Número de coordinación 8 |
Rellenar huecos
Relaciona cada concepto de la serie de letras con uno de la serie numerada, indicando en cada casilla el número correspondiente.