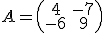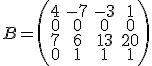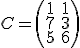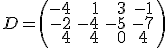4.1. Cálculo del rango por determinantes

Vamos a comenzar ahora a utilizar una técnica para calcular el rango de una matriz mediante determinantes.

Recuerda que para calcular el determinante de una matriz utilizábamos algunos menores que componían la misma. Ahora vamos a hacer algo parecido. No debes perder de vista que, a la hora de calcular el rango de una matriz, debemos indicar el número de filas y el número de columnas (el que sea menor de los dos) que sean linealmente independientes.

Para aplicar esta técnica de cálculo del rango de una matriz lo vamos a hacer a través de un ejemplo. Sabemos que si el determinante de una matriz es cero, sus filas son linealmente dependientes y sus columnas son linealmente dependientes, por lo que vamos a intentar buscar la submatriz de mayor orden cuyo determinante sea distinto de cero y esas filas y columnas que contenga serán linealmente independientes. Observa bien el proceso.

Vamos a calcular el rango de la matriz:

Consideraciones previas:

Sabemos que el rango es ≤3 puesto que tiene 3 filas y 3 columnas. El rango de una matriz va a ser siempre mayor o igual que cero y menor o igual que el mínimo entre el nº de filas y el nº columnas. Luego en este caso el rango puede ser 0, 1, 2 o 3

Cálculo del rango:

• Cogemos un elemento de la matriz distinto de cero, por ejemplo el elemento a₁₁=-1

Como|-1|=-1 ≠0 luego el rango de la matriz ≥1.  El rango puede ser 1 ,2 o 3 (Si todos los elementos de la matriz fueran nulos, estaríamos frente a la matriz nula, cuyo rango sería 0)

• A continuación cogemos una submatriz de orden 2 (2 filas y dos columnas) y calculamos su determinante. Por ejemplo, elegimos la submatriz formada por las 2 primeras filas y las 2 primeras columnas

Calculamos su determinante:

El determinante es -3 y por tanto, distinto de cero.

(Nótese que las matrices se representan entre paréntesis y los determinantes entre barras.)

Como el determinante es distinto de cero, eso garantiza que el rango es≥ 2. El rango puede ser 2 o 3

Si todas las submatrices de orden 2 tuvieran determinante cero, el rango de la matriz  sería 1, y deduciríamos que habría dos filas (columnas) proporcionales a la restante

• Elegimos la matriz completa A y calculamos su determinante:

= (-15+0+0)-(24+0+0)=-29≠0

Como el determinante es distinto de cero,  el rango es 3 y deducimos que ninguna fila (o columna) es combinación lineal de las demás. (Nota: si hubiera sido el determinante igual a cero sería el rango 2, lo que indica que una fila (o columna) se puede poner como combinación lineal de las demás)

Nota: Podríamos haber calculado como primer paso el determinante de la matriz 3x3 y si fuese distinto de cero, concluir ya que su rango es 3, y si fuese cero, buscar alguna submatriz 2x2 cuyo determinante fuese distinto de cero para concluir rango 2 y si no lo hubiera sería rango 1 si existiese algún elemento distinto de cero en la matriz.