3. Cálculo de la matriz inversa mediante determinantes
Importante
Dada una matriz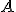 
, la fórmula por la que podemos calcular la inversa de la matriz, si tiene determinante distinto de cero, es:
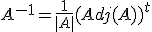
Es decir, la inversa de una matriz es igual a la matriz traspuesta de su adjunta multiplicada por el inverso del determinante
Ejemplo o ejercicio resuelto
Vamos a calcular la matriz inversa de
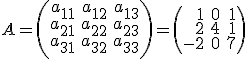
Para ello vamos a aplicar la fórmula que nos han indicado anteriormente:
AV - Reflexión
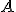por 
resulta lo mismo que multiplicar por y el resultado es la matriz identidad
Practica ahora lo que has aprendido.
1.- Introduce la matriz A de la que quieras calcular su matriz inversa
2.- Recuerda que ahora debes calcular el determinante de la matriz que has introducido ya que solamente se puede calcular la matriz inversa si el determinante es distinto de cero. Cuando lo hayas calculado pulsa sobre el botón Det(A) para comprobar que lo has hecho bien
3.- Ahora debes calcular la matriz adjunta de la matriz A. Cuando lo hayas hecho, pulsa sobre el botón Adj(A) y comprueba si la has calculado bien.
4.- Con los datos que tienes, puedes calcular la matriz inversa. una vez que la hayas calculado, pulsa sobre el botón Inv(A) y comprueba si te ha salido correctamente:
|
Actividad
Si A es una matriz cuadrada nxn cuya inversa esy si X es una matriz incógnita y B una matriz conocida, ambas con n filas, entonces la solución de la ecuación matricial
AX=B
viene dada por
Al resultado anterior se llega de la siguiente forma
AV - Actividad de Espacios en Blanco
Ahora te proponemos un ejercicio más directo en el que observes que podemos resolver ecuaciones con matrices. En este caso la ecuación matricial que te proponemos es la siguiente:
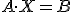
Donde las matrices que aparecen son: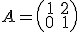 
y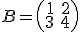 
.