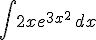2. Calculo de primitivas inmediatas de funciones compuestas

Imagen en Flicker de Shermeee bajo CC

En ocasiones, es necesario integrar funciones compuestas de dos funciones elementales. Para determinar estas integrales, disponemos de una serie de reglas para facilitar nuestra labor.

Las integrales inmediatas para funciones compuestas son análogas a las anteriores como vemos a continuación:

Actividad

Funciones potenciales

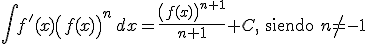
$\int f'(x) \left(f(x)\right)^n \, dx=\frac{\left(f(x)\right)^{n+1}}{n+1}+C,\begin{verbatim}{ siendo }\end{verbatim} n eq -1$

Importante

Funciones trigonométricas:

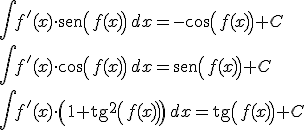
$\int f'(x) \cdot \begin{verbatim}sen\end{verbatim} f(x) \, dx = -\cos f(x) + C \\ \int f'(x) \cdot \cos f(x) \, dx = \begin{verbatim}sen\end{verbatim} f(x) + C \\ \int f'(x) \cdot $1+ \begin{verbatim}tg\end{verbatim}^2 f(x) $ \, dx = \begin{verbatim}tg\end{verbatim} f(x) + C$

Importante

Funciones inversas de las trigonométricas

$\int \frac{f'(x)}{\sqrt{1-f(x)^2}} \, dx = \begin{verbatim}arcsen\end{verbatim} \left( f(x) \right) +C \\ \int \frac{-f'(x)}{\sqrt{1-f(x)^2}} \, dx = \begin{verbatim}arccos\end{verbatim} \left(f(x) \right)+C \\ \int \frac{f'(x)}{1-f(x)^2} \, dx = \begin{verbatim}arctg\end{verbatim} \left(f(x) \right) +C$

Importante

Funciones exponenciales

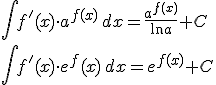
$\int f'(x) \cdot a^{f(x)} \, dx=\frac{a^{f(x)}}{\ln a}+C \\ \int f'(x) \cdot e^f(x) \, dx=e^{f(x)} + C$

Importante

Funciones logarítmicas

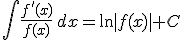
$\int \frac{f'(x)}{f(x)} \, dx =\ln |f(x)|+C$

Veamos algún ejemplo:

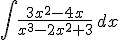
$\int \frac{3x^2-4x}{x^3-2x^2+3} \, dx$

Hay que darse cuenta de que la función que está en el numerador es la derivada de la que está en el denominador entonces atendiendo a la fórmula:

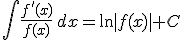
$\int \frac{f'(x)}{f(x)} \, dx =\ln |f(x)|+C$

Por lo que quedaría:

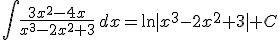
$\int \frac{3x^2-4x}{x^3-2x^2+3} \, dx = \ln | x^3-2x^2+3 | + C$

Por tanto básicamente lo que hay que buscar con este tipo de integrales es la función y su derivada, o "algo parecido", y aplicar alguna de las fórmulas anteriores.

Veamos que queremos decir con lo de "algo parecido" a la derivada.

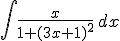
$\int \frac{x}{1+(3x+1)^2} \, dx$

En esta función aparece una función como 3x+1 y algo parecido a su derivada x, para integrar actuamos de la siguiente forma:

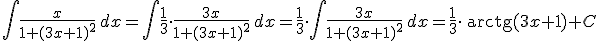
$\int \frac{x}{1+(3x+1)^2} \, dx = \int \frac{1}{3} \cdot \frac{3x}{1+(3x+1)^2} \, dx = \frac{1}{3} \cdot \int \frac{3x}{1+(3x+1)^2} \, dx = \frac{1}{3} \cdot\begin{verbatim} arctg\end{verbatim}(3x+1) +C$

Lo que hacemos es transformar la x en la derivada de la función y como para transformarla tenemos que multiplicar, dividimos por el mismo número. La fracción numérica resultante la extraemos de la raíz por una de las propiedades anteriores con lo que queda la integral anterior.