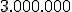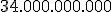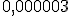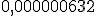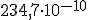5. Notación científica

Pre-conocimiento

un sol mirando con lupa a la tierra, quemándola un poco

Imagen en Flickr de Almudena Fndez bajo CC

¿Te has planteado alguna vez a qué distancia estamos del Sol?

Seguro que sí, y seguro que has visto alguna vez la solución, aunque ahora mismo no la recuerdes.

Estamos a ciento cincuenta millones de kilómetros, chispa más o menos, porque con esa cantidad no nos vamos a plantear las decenas de kilómetros, ni los metros, o sea, evidentemente es una aproximación (recuerda el apartado anterior).

Pero ahora lo que nos ocupa es la cantidad, esto es, los ciento cincuenta millones de kilométros, que en números es algo así como: 150000000 km. ¡Vaya tela!, ¡imagínate escribir la distancia del Sol a Plutón! Te preguntarás, ¿y cómo los matemáticos no se han planteado escribirlo más cómodamente, más pequeño? Pues sí, lo hemos hecho, podemos escribirlo así: 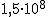km.

Para poder escribir esta cantidad de esta manera, hay que saber utilizar la segunda parte del nombre de este tema, la notación científica; y para saber utilizar la notación científica es necesario conocer y dominar lo estudiado en el tema 1 sobre las potencias.

Vayamos pues, paso a paso, a ser capaz de escribir cantidades tan grandes.

O tan pequeñas, porque si nos planteamos la masa de un electrón, a ver como la expresas ¿con 31 ceros en los decímales? no, más bien con las potencias y la notación científica.

La masa de un electrón es: 0,00000000000000000000000000000091 kg, uff, que pasada, fíjate ahora: kg; ¿mejor verdad?

Imagen en Wikimedia Commons de Thalia Inga bajo CC

Como hemos visto al principio del tema, hay números que son tan grandes o tan pequeños que resulta difícil nombrarlos y escribirlos y por eso nos ayudamos de las potencias para expresarlos de forma más simplificada. La notación científica es una forma particular de escribir estos números utilizando las potencias.

Así la forma de expresar la distancia de la Tierra al Sol como 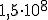km, o la masa de un electrón como 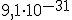kg se llama notación científica.

Actividad

Una cantidad se expresa en notación científica como un número por una potencia de 10 (de exponente positivo o negativo). Dicho número tiene que cumplir unas condiciones:

Si es entero tiene que tener una sola cifra, por ejemplo: .
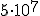Si es decimal, la parte entera tiene que tener una sola cifra del 1 al 9, es decir, la parte entera no puede ser cero.

Por ejemplo la cantidad

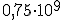no está expresada en notación científica pues la parte entera del número es un cero. Sin embargo la cantidad

sí está bien expresada en notación científica pues la parte entera del número es una cifra comprendida entre 1 y 9.

Veamos algunos ejemplos que nos pueden ayudar a la hora de expresar un número en notación científica, en los que se observa que al multiplicar un número por una potencia de 10 de exponente positivo, lo que hacemos es multiplicar por la unidad seguida de tantos ceros como indique el exponente, mientras que al multiplicar por una potencia de 10 de exponente negativo, lo que hacemos es dividir por la unidad seguida de tantos ceros como indique el exponente:





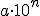
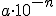
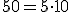
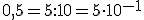
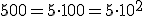
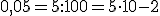
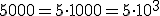
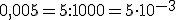
50000 = 5 · 10000 = 5 · 10⁴	0,0005 = 5 : 10000 = 5 ·10^-4
500000 = 5 · 100000 = 5 · 10⁵	0,00005 = 5 : 100000 = 5 · 10^-5
5000000 = 5 · 1000000 = 5 · 10⁶	0,000005 = 5 : 1000000 = 5 · 10^-6