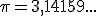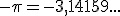3. Expresión decimal aproximada de un número real
Cuando escribimos un número decimal infinito, estamos representando, como su nombre indica, un número que tiene infinitas cifras decimales. Pero al vernos en la imposibilidad de escribir las infinitas cifras, representamos el número sólo con un cierto número de ellas, por lo que estamos cometiendo un error.
Por ejemplo, tenemos el número real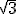 
; si efectuamos la raíz podemos obtener tantas cifras decimales como queramos: 
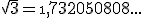Podemos realizar las siguientes aproximaciones de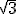
Aproximación hasta las décimas.
Podemos coger como valor aproximado de 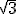o bien 
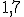o 
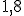ya que 
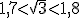en este caso estamos cometiendo un error menor de 
.
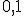Si cogemos como valor aproximado 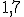estamos cometiendo un error por defecto ya que: 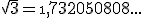y se cumple que:
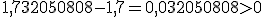
Si cogemos como valor aproximado 1,8 estamos cometiendo un error por exceso ya que: 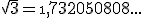y se cumple que:
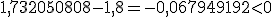
Aproximación hasta las centésimas.
Podemos coger como valor aproximado de 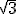o bien 
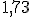o 
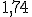ya que 
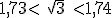en este caso estamos cometiendo un error menor de 
.
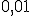Si cogemos como valor aproximado 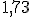estamos cometiendo un error por defecto ya que: 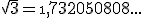y se cumple que:
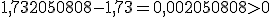
Si cogemos como valor aproximado 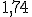estamos cometiendo un error por exceso ya que: 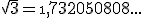y se cumple que:
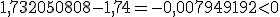
Y así sucesivamente.
A partir de ahora al valor exacto de un número real lo designaremos por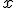 
, y al valor aproximado por 
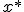, es decir, en el ejemplo de la
aproximación hasta las décimas de arriba en el caso de que elijamos
como valor aproximado .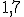
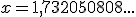
Actividad
Cuando
aproximamos estamos cometiendo un error, siendo éste la diferencia entre el valor
exacto y el aproximado. Este error se llama absoluto y lo denotaremos por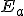 
,
y como hemos explicado su valor es:
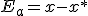
Según el signo de Ea podemos distinguir entre error por exceso o por defecto:
- Si
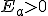error por defecto; la aproximación es más pequeña que el valor real.
- Si
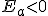error por exceso; la aproximación es mayor que el valor real.
Importante
El error relativo en la aproximación es el
cociente entre el error absoluto y el valor exacto, se denota como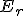 
.
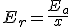
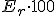
A la hora de aproximar se utilizan dos tipos de aproximaciones:
- Truncamiento
- Redondeo
Actividad
Truncamiento
El truncamiento consiste en cortar el número exacto sin preocuparnos de cómo continúa la expresión decimal después.
Ejemplo: Jesús tiene en realidad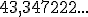 
años pero el sólo responde 
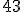. Lo que acaba de hacer es un truncamiento.
Actividad
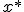es más pequeño que el valor
exacto ;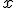
.
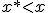Como has visto, los años de Jesús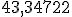 
es mayor que la aproximación que se utiliza por truncamiento.
La aproximación por truncamiento (en números negativos) siempre es por exceso, es decir,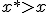 
.
Actividad
Redondeo
En el redondeo la
aproximación puede ser por defecto o por exceso, depende del valor de la cifra
siguiente a la que aproximamos.
De esta forma:
- Si la cifra siguiente al orden de aproximación es menor que 5 la aproximación por redondeo es la misma que la de truncamiento y por tanto la aproximación es por defecto.
- Si la cifra siguiente al orden de aproximación es mayor o igual que 5 la aproximación por redondeo es por exceso, con lo que sumamos una unidad a la última cifra decimal que ponemos.
Caso de estudio
