1.1. Los números irracionales
Como has visto ya en el tema 1, el hombre inventó en primer lugar los números naturales para contar. Más tarde tuvo necesidad de medir e inventó los números decimales y las fracciones. Se sabe que los babilonios conocían ya estos tipos de números. Y la verdad es que en la práctica diaria, estos números resuelven todos los problemas de medidas.
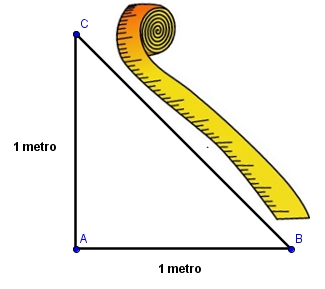
Fuente propia realizada con geogebra bajo Dominio público
|
Construyamos, por ejemplo, un triángulo rectángulo como el de la figura y supongamos que los catetos miden 1 metro cada uno. Si nos disponemos a medir con una cinta métrica la hipotenusa, llegaremos al resultado:
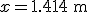
Como las cintas métricas están graduadas hasta los milímetros, hemos conseguido una aproximación de la medida hasta esta unidad. Con otro aparato de medida más exacto hubiéramos podido aproximarnos más a la medida exacta.
Ahora bien, podemos plantearnos la siguiente pregunta, ¿es la medida exacta de la hipotenusa un decimal finito? Podría parecer en principio que, efectivamente, esto es así. Pero veámoslo ahora desde un punto de vista más fino, haciendo uso de las propiedades geométricas del triángulo de la figura:
Utilizando el Teorema de Pitágoras, llegamos a la conclusión de que:
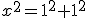 es decir,
es decir, 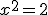
Hemos conseguido, de esta forma, saber que la hipotenusa mide una longitud 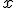 que elevada al cuadrado da 2. A ese número
que elevada al cuadrado da 2. A ese número 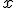 solemos llamarlo "raíz cuadrada de 2" y lo designamos con el símbolo
solemos llamarlo "raíz cuadrada de 2" y lo designamos con el símbolo 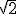 .
.
Pero 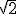 no es más que un símbolo para denotar un número decimal. Hay varios procedimientos para hallar los decimales de este número. Todos ellos nos proporcionan un número decimal infinito. Con una calculadora de bolsillo obtenemos:
no es más que un símbolo para denotar un número decimal. Hay varios procedimientos para hallar los decimales de este número. Todos ellos nos proporcionan un número decimal infinito. Con una calculadora de bolsillo obtenemos:
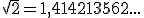
Ponemos puntos suspensivos para indicar que hay más cifras decimales que no escribimos. De hecho si queremos construir algo de medida 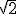 nos sobra con las cifras decimales que hemos escrito. Así pues, como primera conclusión:
nos sobra con las cifras decimales que hemos escrito. Así pues, como primera conclusión:
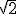 es un decimal infinito.
es un decimal infinito.
Podemos avanzar un poco más en nuestro estudio. Hasta ahora los decimales infinitos que conocemos son los decimales infinitos periódicos que, como ya sabemos, son en realidad números racionales o fracciones. Así surge de manera natural la pregunta:
¿Es 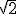 un decimal infinito periódico?
un decimal infinito periódico?
Si así fuera, el número raíz de 2, a pesar de su extraña apariencia, no sería más que un número racional; algo ya conocido. Precisamente eso creyeron los griegos durante algún tiempo. Pero no es así; probaron que 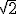 no es una fracción ni, naturalmente, un decimal infinito periódico. Así pues:
no es una fracción ni, naturalmente, un decimal infinito periódico. Así pues:
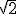 es un decimal infinito no periódico: no es un número racional.
es un decimal infinito no periódico: no es un número racional.
Pero, desde el punto de vista de la teoría, 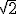 nos hace falta y, como no es un número racional, hay que bautizarlo. Lo llamaremos número irracional.
nos hace falta y, como no es un número racional, hay que bautizarlo. Lo llamaremos número irracional.
Actividad
La cantidad de números irracionales es infinitamente mayor que la de los racionales. Entre ellos están las raíces cuadradas de los números que no son cuadrados perfectos, como ![]() . Y otros tan famosos como el número
. Y otros tan famosos como el número 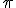 .
.
Actividad
Los números irracionales se clasifican en dos tipos:
- Números algebraicos: Resultan de la solución de alguna ecuación algebraica con coeficientes enteros. Todas las raíces no exactas de cualquier orden son irracionales algebraicos. Por ejemplo, el número áureo es una de las raíces de la ecuación algebraica
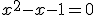 , por lo que es un número irracional algebraico.
, por lo que es un número irracional algebraico. - Números trascendentes: No son solución de alguna ecuación algebraica con coeficientes enteros. Provienen de las llamadas funciones trascendentes (trigonométricas, logarítmicas y exponenciales, etc.). También surgen al escribir números decimales no periódicos al azar o con un patrón que no lleva periodo definido, respectivamente, como los dos siguientes: 0,19365027844375... o 0,10100100010000...
Los llamados números trascendentes tienen especial relevancia ya que no pueden ser solución de ninguna ecuación algebraica. Los números pi (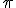 ) y e son irracionales trascendentes, puesto que no pueden expresarse mediante radicales.
) y e son irracionales trascendentes, puesto que no pueden expresarse mediante radicales.
Fuente: Wikipedia