4. Introducción a las inecuaciones

Importante

Dados dos números reales cualesquiera, a y b, se pueden dar estas tres situaciones:
  • a < b ; a menor que b. A la expresión la llamamos desigualdad
  • a = b ; a igual que b. A la expresión la llamamos igualdad
  • a > b ; a mayor que b. A la expresión la llamamos desigualdad 

Esta propiedad que cumplen todos los números reales, hace que su conjunto, el conjunto de los números reales, sea totalmente ordenado. Hablamos entonces, del orden de los números reales.

Otra forma de visualizar las desigualdades y el orden de los números reales sería:

Balanzas con pesas
Fuente propia realizada bajo Dominio público

 

3 6 5
Fotografía en Flick de nataliej bajo CC

 

Cuando se tiene una nueva propiedad sobre el conjunto de los números reales, lo primero que debe plantearse es cómo actúa esta propiedad con las operaciones básicas que tenemos en nuestro conjunto, que son: la suma y el producto. Evidentemente, cuando decimos suma, estamos incluyendo a la resta, y cuando decimos producto, también hablamos de la división.

Y esto es lo que vamos a ver en este apartado. Para ello vamos a separarlos en dos epígrafes, y te vamos a pedir que seas tú, quien mediante unas actividades, vayas descubriendo cómo se comporta nuestro recién estrenado orden de los números reales, con las ya conocidas operaciones, suma y producto.

Caso de estudio

Vamos a estudiar cómo se comporta el orden de los números reales y la suma. Para ello, vamos a realizar varios ejercicios, de manera que sumemos tanto números positivos como negativos a una desigualdad, para comprobar si se mantiene la desigualdad una vez hayamos realizado la suma.
Aplica a la desigualdad 3< 5, las siguientes transformaciones.

 

  1. Suma 2 a cada uno de los miembros de la desigualdad y comprueba si es cierta.
  2. Suma ahora 1,72 a cada miembro y comprueba.
  3. Suma esta vez -5 a cada miembro, y verifica si se mantiene la desigualdad.

Una vez realizado los tres apartados, debes llegar a una conclusión, y activar la opción "Ver solución" para comprobar que estás en lo cierto.

Balanzas para suma
Fuente propia realizada bajo Dominio público

Caso de estudio

Escribe las siguientes informaciones utilizando las desigualdades: (comprueba las soluciones)
  1. He sacado en el último control de matemáticas, al menos un 7.
  1. La tarifa de mi móvil es plana desde las 10 de la mañana hasta las 6 de la tarde.
  1. La edad del seleccionador español Vicente Del Bosque es 59 años, cifra que supera las edades de Busquet y Javi Martínez (ambos tienen 21)
  1. Como todo el mundo sabe el valor del número real 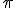es menor que 4.
Por último, debemos mencionar que si multiplicamos los dos miembros de una desigualdad por 0, la desigualdad deja de tener sentido.

Caso de estudio

A continuación te proponemos una serie de ejercicios que te deben llevar a descubrir dos propiedades de las desigualdades. Lo que debes hacer es multiplicar (o dividir) los dos miembros de una desigualdad, y comprobar si se mantiene o no.
Dada la siguiente desigualdad: 2 < 5. Realiza:
  1. Multiplica los dos miembros por 3, y comprueba si se mantiene la desigualdad.
  2. Multiplica ahora por 4,5 y vuelve a comprobar.
  3. Multiplica esta vez por 1/2, o lo que es lo mismo, divide por 2 ambos miembros, y comprueba la desigualdad.

Una vez hayas hecho los tres apartados y hayas llegado a una conclusión, pincha en "Ver solución" y comprueba.

Veamos ahora que ocurre cuando multiplicamos por un número negativo. Sea la desigualdad: 2 < 4. Realiza:
  1. Multiplica por -1, y comprueba a ver si se mantiene la desigualdad o se obtiene otra distinta.
  2. Multiplica ahora por -4, y vuelve a comprobar.
  3. Divide ahora por -2, a ver que ocurre.

Cuando hayas llegado a una conclusión, pincha en "Ver solución", y obtén la propiedad adecuada.

Importante

Propiedades de las desigualdades

Sean a, b y c tres números reales.

  1. Si a<b, entonces a+c<b+c para cualquier número c.
  2. Si a<b, entonces a·c<b·c para cualquier número c>0.
  3. Si a<b, entonces a·c>b·c para cualquier número c<0.

Las desigualdades no se comportan igual que las igualdades cuando multiplicamos ambos términos por un mismo número.