3. Clasificación de los sistemas de ecuaciones lineales en función del número de soluciones que presentan
Importante
Un sistema de ecuaciones lineales se dice que es compatible si tiene solución y en caso contrario se llama incompatible.
Si el sistema tiene una única solución recibe el nombre de dompatible determinado. Si tiene infinitas soluciones se llama compatible indeterminado.

|
Por ejemplo. El siguiente sistema de ecuaciones:
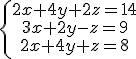
|
Cuya solución es: x=7, y=-3, z=6 es compatible determinado ya que presenta una única solución según el anterior esquema.
En estos otros ejemplos:
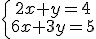
|
El sistema no tiene solución por lo que es incompatible.
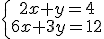
|
En este otro caso el sistema presenta infinitas soluciones por lo que lo llamamos compatible indeterminado.
Para comprobar la compatibilidad e incompatibilidad de un sistema de ecuaciones hemos de resolverlo antes por cualquier método, la existencia o no de solución nos determinará la clase de sistema ante el cual nos encontramos. En el caso de sistemas de dos ecuaciones con dos incógnitas también podemos seguir la siguiente regla.
Importante
 Fuente propia bajo Dominio público |
Para saber el número de soluciones de un sistema lo haremos a partir de los coeficientes de las incógnitas.
Recordemos el sistema de ecuaciones genérico que vimos anteriormente:
|
|
| Si |
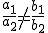
|
el sistema tiene una única solución y se llama sistema compatible determinado (SCD). |
| Si |
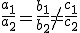 |
el sistema no tiene solución y se llama sistema incompatible (SI). |
| Si |
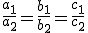 |
el sistema tiene infinitas soluciones y se llamas sistema compatible indeterminado (SCI). |
Caso de estudio
Comprueba el número de soluciones de los siguientes sistemas de ecuaciones:
| a) |
|
| b) | |
| c) | |
Pregunta de Elección Múltiple
Importante
Si resolvemos gráficamente un sistema de ecuaciones, es decir, si representamos gráficamente las rectas que lo forman pueden ocurrir los siguientes casos:
- Las dos rectas se cortan en un punto, entonces, ese punto es la solución del sistema y el sistema es compatible determinado.
- Las dos rectas son paralelas, entonces, no se cortan en ningún punto, por tanto, el sistema no tiene solución, es incompatible.
- Las dos rectas resultan ser la misma recta, es decir, se cortan en infinitos puntos, por tanto el sistema tiene infinitas soluciones, es compatible indeterminado.
Te puede servir de ayuda para entender esto una de las escenas de GeoGebra que aparecen en el apartado de método de resolución gráfico.
Pregunta de Elección Múltiple
Para practicar
- Puedes practicar los conceptos aprendidos realizando los dos primeros test de la parte de Clasificación de la página de Álgebra con papas.