2.2. Sistemas equivalentes. Método de Gauss
Importante
Decimos que dos sistemas de ecuaciones son equivalentes cuando ambos tienen la misma solución.
Por ejemplo:
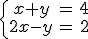
|
y |
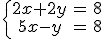 |
son equivalentes ya que ambos tienen la misma solución: x=2, y=2.
Veamos otro ejemplo.
Los sistemas de ecuaciones vistos en el apartado anteriores
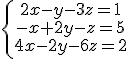
|
y |
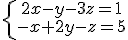 |
son equivalentes, ambos tienen las mismas infinitas soluciones.
El concepto de sistemas equivalentes es la base de los métodos de resolución de sistemas de ecuaciones, en concreto del método de reducción y del de Gauss, este último para sistemas de tres ecuaciones con tres incógnitas.
Para transformar un sistema en otro equivalente podemos seguir las siguientes reglas.
Importante
- Si en un sistema de ecuaciones se cambia el orden de las ecuaciones o el orden de las incógnitas, el sistema resultante es equivalente al primero.
- Si la ecuación ax+by=c se multiplica o divide por un número
distinto de cero, la ecuación resultante es equivalente a la anterior.
Por ejemplo la ecuación 10x+5y=25 es equivalente a la ecuación 2x+y=5 que se ha obtenido dividiendo todos los coeficientes entre 5. - Si en un sistema a una ecuación se le suma o resta otra ecuación distinta (las cuales pueden estar multiplicadas por distintos números), el sistema resultante es equivalente al primero.
|
|
y sustituimos la segunda ecuación por la que se obtiene restando a la de arriba la de abajo,
|
|
el nuevo sistema que resulta
|
|
es equivalente al primero.
Por último en el siguiente enlace puedes estudiar con más profundidad las reglas vistas más arriba sobre sistemas equivalentes.
Sistemas escalonados

|
Un sistema de ecuaciones lineales se llama escalonado cuando los coeficientes de las incógnitas de las ecuaciones que lo componen se van haciendo todos ceros hasta que en la última ecuación queda solo una incógnita con un coeficiente distinto de cero.
Ejemplos de sistemas escalonados son los siguientes:
| o | 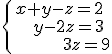 |
Estos sistemas son muy fáciles de resolver. Basta con despejar una incógnita en una de las ecuaciones en la que solo queda esta y ir sustituyendo en las siguientes para hallar el valor del resto de las incógnita. El método de Gauss que se expondrá más adelante consiste en convertir un sistema de ecuaciones lineales en un sistema escalonado que es más facil de resolver.
Reflexión
Vamos a practicar antes de seguir.
Resuelve los sistemas:
| a. |
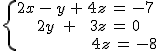
|
b. |
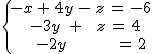 |
Importante
Método de Gauss
Este método consiste en transformar el sistema que queremos resolver en otro escalonado equivalente.
Para conseguirlo podemos usar las siguientes transformaciones ya vistas en el apartado anterior:
- Cambiar de orden dos ecuaciones.
- Multiplicar o dividir los dos miembros de una ecuación por un mismo número.
- Cambiar una ecuación por la suma de esta más otra ecuación.
Si te fijas, estas transformaciones son las mismas que se aplicaban en el apartado 1.3 cuando resolvíamos un sistema por el método de reducción. Había que multiplicar las ecuaciones por números para que cuando las sumaras una de las incógnitas se fueran.
Vamos a ver con un ejemplo, cómo se resuelve un sistema utilizando este método.
Caso de estudio
Resolver el siguiente sistema por el método de gauss:
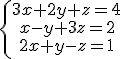
|
La siguiente escena de GeoGebra te puede ayudar a entender la resolución de los ejercicios que aparecen en este apartado. Mueve los deslizadores que aparecen en la parte superior de la escena para seleccionar los coeficientes de cada ecuación.
Cada ecuación se corresponde con cuatro deslizadores en sentido vertical, y los coeficientes se van seleccionando de arriba abajo, siendo el superior el de la x, el siguiente el de la y, etc. La primera ecuación se corresponde con los primeros 4 deslizadores de la izquierda.
En la parte de la derecha aparece el sistema de ecuaciones tal como va quedando a medida que vas seleccionando los coeficientes. Cuando los hayas seleccionado todos te aparecerán abajo los sistemas equivalentes al que quieres resolver, siendo el último de la derecha el sistema escalonado.
En la parte inferior izquierda aparecen las soluciones del sistema, en el caso de que este las tenga. Los términos de sistema compatible e incompatible se explican en el apartado 3 de este tema.
La resolución en forma matricial es un procedimiento de aplicación del método de Gauss que no corresponde al nivel de este curso y que no resulta necesario para su comprensión.
Si no puedes ver esta escena de geogebra accede a la siguiente página.
En el siguiente enlace puedes ver otro ejemplo de resolución de sistemas de 3 ecuaciones con tres incógnitas por el método de Gauss.
Actividad de rellenar huecos
Completa los cuadros en blanco con los números y signos que correspondan.
Ojo: No dejes espacios en blanco entre los signos y los números. Escríbelo todo seguido.
Pregunta de Selección Múltiple
Solution
Solution
Pregunta de Elección Múltiple
Reflexión
Encuentra la solución de los siguientes sistemas usando el método de Gauss:
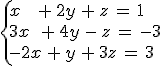
|
y | 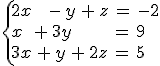 |
Dos casos especiales. Cuando el sistema tiene infinitas soluciones o no tiene solución
- Sistema con infinitas soluciones.
Todos los sistemas del punto anterior podían resolverse y encontrábamos una solución para cada incógnita. Es decir, el sistema tiene una única solución.
Hay veces en las que a pesar de tener tres ecuaciones en el sistema, una de ellas no aporta ninguna información nueva; no añade nada nuevo, por lo que en realidad tenemos dos ecuaciones y por tanto infinitas soluciones para el sistema.
Esto ocurre cuando al aplicar el método de Gauss en el último paso, sucede que se van todas las incógnitas y los términos independientes, es decir, llegamos al caso en el que la última ecuación queda:
0=0
Como esto siempre es verdad, volvemos a insistir en que el sistema tendrá infinitas soluciones.
El siguiente ejercicio resuelto muestra un ejemplo de este tipo.
Caso de estudio
Vamos a resolver el siguiente sistema y vamos a ver que ocurre lo que acabamos de comentar:
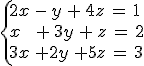
- Sistema sin ninguna solución.
 Imagen en Flickr de chrispy1in200611 bajo CC Imagen en Flickr de chrispy1in200611 bajo CC
|
En este caso llegamos a una expresión de la forma:
0 = K, siendo K un número distinto de cero.
Como eso no es verdad, llegamos a la conclusión que el sistema no tiene solución. El siguiente ejercicio resuelto muestra un ejemplo de este tipo.
Caso de estudio
Vamos a ver que el siguiente sistema no tiene solución:
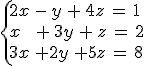
|