1.2. Métodos de resolución: Método gráfico

En primer lugar tenemos que ver como se realiza la representación gráfica de una ecuación lineal con dos incógnitas, para ello observa la siguiente presentación, pulsando con el cursor del ratón sobre la pantalla podrás ir pasando de una diapositiva a otra.

Fuente propia bajo Dominio público

Desde este enlace puedes descargar la presentación en tu ordenador y verla si tienes instalado el programa Impress o Microsoft Power Point. La representación gráfica de una ecuación lineal con dos incógnitas es siempre una recta. En la siguiente escena de geogebra puedes ver la representación gráfica de distintas ecuaciones lineales, para ello mueve los deslizadores situados en la parte superior izquierda para representar distintas ecuaciones. Te puede servir para comprobar que las representaciones que haces en tu cuaderno o en un folio son correctas.

Si no puedes ver esta escena de Geogebra accede a la siguiente página.

A la hora de resolver un sistema de dos ecuaciones con dos incógnitas por el método gráfico se procede de la siguiente forma.

Por ejemplo, consideremos el sistema:

Vamos a despejar la "y" de cada una de las ecuaciones:

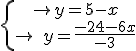Ahora, en una tabla, daremos valores a la "x", y realizando las operaciones obtendremos los correspondientes valores de la "y". Así, conseguiremos las coordenadas (x, y) de algunos puntos de cada recta, y uniéndolos obtendremos sus gráficas.



0	5
1	4
-1	6



0	8
1	10
-1	6

La solución del sistema es el punto donde se cortan las dos rectas, como podemos ver en la tabla, dicho punto es A(-1, 6), es decir, la solución es: x = -1 y = 6.

Veamos la representación gráfica de este sistema y su solución, hemos llamado "a" a la recta: , "b" a la recta: , y A(-1, 6) es el punto de corte de las dos rectas a y b.

Fuente propia bajo Dominio público

Dos casos especiales: Cuando el sistema no tiene solución o tiene infinitas soluciones

A la hora de resolver un sistema de ecuaciones por el método de reducción pueden surgir los siguientes casos:

El sistema no tiene solución.

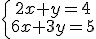
No existen unos valores de x e y para los cuales se cumplan simultáneamente las ecuaciones del sistema. Al resolver un sistema de ecuaciones por el método gráfico aparecen dos rectas que son paralelas y no presentan ningún punto de corte. En el siguiente ejemplo:

Si lo resolvemos con la aplicación de geogebra que aparece más abajo, podrás comprobar cómo las rectas, que son la representación gráfica de cada una de las ecuaciones del sistema, son paralelas y no se cortan. Esto indica que el sistema no tiene solución.

El sistema tiene infinitas soluciones.

En este caso el sistema admite como solución infinitos valores de x e y. Al resolver el sistema por el método gráfico aparecen dos rectas que se superponen una encima de otra. En el siguiente ejemplo:

Si lo resolvemos con la aplicación de geogebra que aparece más abajo podrás comprobar cómo las rectas, que son la representación gráfica de cada una de las ecuaciones, coinciden una con otra formando una sola. Esto nos indica que el sistema tiene infinitas soluciones (cada uno de los puntos de las dos rectas coincidentes).

Si no puedes ver esta escena de geogebra accede a la siguiente página.