1.1. Métodos de resolución: Método de sustitución, igualación y reducción
Los métodos clásicos de resolución de los sistemas de dos ecuaciones con dos incógnitas son: El método de sustitución, de igualación y el de reduccción. Empezamos con el de sustitución.
Importante
- En una de las ecuaciones se despeja una de las incógnitas en función de la otra.
- La incógnita despejada se sustituye en la otra ecuación, con lo que obtenemos una ecuación donde solo hay una incógnita.
- Se resuelve esta ecuación obteniendo el valor de una de las incógnitas.
- Se sustituye en la expresión hallada en el paso 1 la incógnita cuyo valor hemos obtenido en el paso 3 por este y se obtiene la otra incógnita.
Ahora puedes comprobar cómo se aplica el método en un ejemplo, recorriendo la siguiente presentación. Recuerda hacer clic en las flechas de abajo para pasar a la siguiente diapositiva.
|
|
Puedes seguir practicando este método en el siguiente enlace.
Caso de estudio
Resuelve el siguiente sistema por el método de sustitución:
|
Dos casos especiales: Cuando el sistema no tiene solución o tiene infinitas soluciones
A la hora de resolver un sistema de ecuaciones pueden surgir los siguientes casos:
- El sistema no tiene solución.
No existen unos valores de x e y para los cuales se cumplan simultáneamente las ecuaciones del sistema. Al resolver un sistema de ecuaciones por el método de sustitución llegamos a una contradicción del tipo: 0=1, 1=2, etc. Veamos el siguiente ejemplo:
 |
 |
El resultado final 12=5 es una contradicción de ahí que el sistema anterior no tiene solución.
- El sistema tiene infinitas soluciones.
En este caso el sistema admite como solución infinitos valores de x e y. Al resolver el sistema por el método de sustitución llegamos a una identidad del tipo: 0=0, 1=1, etc. Veamos el siguiente ejemplo.
|
|
El resultado 12=12 es una identidad, de ahí que el sistema admite infinitas soluciones, para hallar algunas lo único que tenemos que hacer es tomar la ecuación 
y darle valores a la x, por ejemplo:
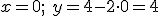Una solución es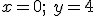 
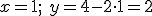otra solución es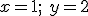 
y así sucesivamente podríamos encontrar tantas soluciones como quisiéramos.
Pregunta de Elección Múltiple
Importante
- Despejamos en las dos ecuaciones la misma incógnita.
- Igualamos entre sí las dos incógnitas despejadas. De esa manera obtenemos una ecuación donde sólo aparece la otra incógnita.
- Se resuelve la ecuación obtenida. Así tenemos el valor de una de las incógnitas.
- Se sustituye la incógnita cuyo valor hemos encontrado en el paso 3. por este en cualquiera de las dos expresiones despejadas en el paso 1 y se halla el valor de la otra incógnita.
Ahora puedes comprobar cómo se aplica el método en un ejemplo, recorriendo la siguiente presentación. Recuerda hacer clic en las flechas de abajo para pasar a la siguiente diapositiva.
|
|
Puedes ver ejemplos de resolución de sistemas de ecuaciones por el método de igualación aquí.
Dos casos especiales: Cuando el sistema no tiene solución o tiene infinitas soluciones
A la hora de resolver un sistema de ecuaciones pueden surgir los siguientes casos:
- El sistema no tiene solución.
No existen unos valores de x e y para los cuales se cumplan simultáneamente las ecuaciones del sistema. Al resolver un sistema de ecuaciones por el método de igualación llegamos a un contradicción del tipo: 0=1, 1=2, etc. Veamos el siguiente ejemplo:
|
 |
 |
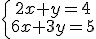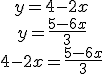El resultado final 12=5 es una contradicción de ahí que el sistema anterior no tiene solución.
- El sistema tiene infinitas soluciones.
En este caso el sistema admite como solución infinitos valores de x e y. Al resolver el sistema por el método de igualación llegamos a una identidad del tipo: 0=0, 1=1, etc. Veamos el siguiente ejemplo.
|
|
|
|
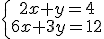
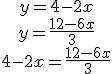
El resultado 0=0 es una identidad, de ahí que el sistema admite infinitas soluciones, para hallar algunas lo único que tenemos que hacer es tomar la ecuación 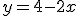y darle valores a la x, por ejemplo:
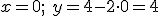Una solución es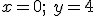
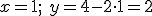otra solución es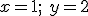
y así sucesivamente podríamos encontrar tantas soluciones como quisiéramos.
Pregunta de Elección Múltiple
Importante
Los pasos a seguir en el método de reducción son los siguientes:
- Se multiplican una o las dos ecuaciones por números convenientes (que debes elegir tú) para que nos queden dos ecuaciones en las que una de las incógnitas vaya multiplicada por el mismo número cambiado de signo.
- Se suman las dos ecuaciones término a término (ya sabes, los términos semejantes entre sí).
- Tras el paso anterior nos queda una ecuación con una sola incógnita. La resuelves como hiciste en el tema 2.
- El valor de la incógnita resuelta se sustituye en cualquiera de las dos ecuaciones primeras y nos queda una ecuación con una sola incógnita, la que aún no sabemos. Se resuelve y ya tienes la solución completa del sistema.
|
|
Puedes practicar el método de reducción en los ejemplos que hay en el siguiente enlace. Resuelve tu primero el sistema y después comprueba si has hecho los cálculos correctos.
Dos casos especiales: Cuando el sistema no tiene solución o tiene infinitas soluciones
A la hora de resolver un sistema de ecuaciones por el método de reducción pueden surgir los siguientes casos:
- El sistema no tiene solución.
No existen unos valores de x e y para los cuales se cumplan simultáneamente las ecuaciones del sistema. Al resolver un sistema de ecuaciones por el método de reducción llegamos a un contradicción del tipo: 0=1, 1=2, etc. Veamos el siguiente ejemplo:
|
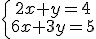Si multiplicamos la primera ecuación por -3 y la sumamos a la segunda obtenemos:
 |
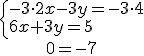El resultado final 0=-7 es una contradicción de ahí que el sistema anterior no tiene solución.
- El sistema tiene infinitas soluciones.
En este caso el sistema admite como solución infinitos valores de x e y. Al resolver el sistema por el método de reducción llegamos a una identidad del tipo: 0=0, 1=1, etc. Veamos el siguiente ejemplo.
|
|
|
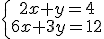
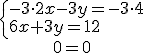
El resultado 0=0 es una identidad, de ahí que el sistema admite infinitas soluciones, para hallar algunas lo único que tenemos que hacer es tomar la ecuación 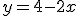y darle valores a la x, por ejemplo:
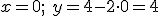Una solución es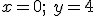
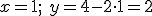otra solución es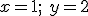
y así sucesivamente podríamos encontrar tantas soluciones como quisiéramos.
Pregunta de Elección Múltiple
PARA PRACTICAR
Este método puedes practicarlo en el siguiente enlace. Encontrarás varias actividades dentro del método de reducción. La primera repasa un poco el método y las demás siguen todas un mismo patrón, tienen un sistema medio resuelto y te van preguntando elementos que faltan. Practica lo que creas convenientes.