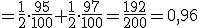3.2. Teorema de la probabilidad total
Vamos a ver la ley fundamental que permite calcular probabilidades de sucesos que dependen de distintas situaciones. Comenzaremos con un ejemplo típico de estas situaciones.
Ejemplo:
Lanzamos un dado cúbico. Si sale 1 ó 2 extraemos una bola de una bolsa, que denominamos A, la cual contiene 6 bolas rojas y 3 azules. Si sale en el dado 3, 4, 5 ó 6 se extrae una bola de una bolsa, que denominamos B, esta contiene 4 bolas rojas y 5 azules.
Como puedes suponer, la probabilidad de obtener una bola roja depende de la bolsa de la que la hayamos sacado y eso depende del resultado del dado. Una forma fácil de resolver este tipo de ejercicios es construir un diagrama de árbol y asignar probabilidades a cada una de sus ramas. Lo podemos ver en la siguiente presentación:
Esquema en árbol
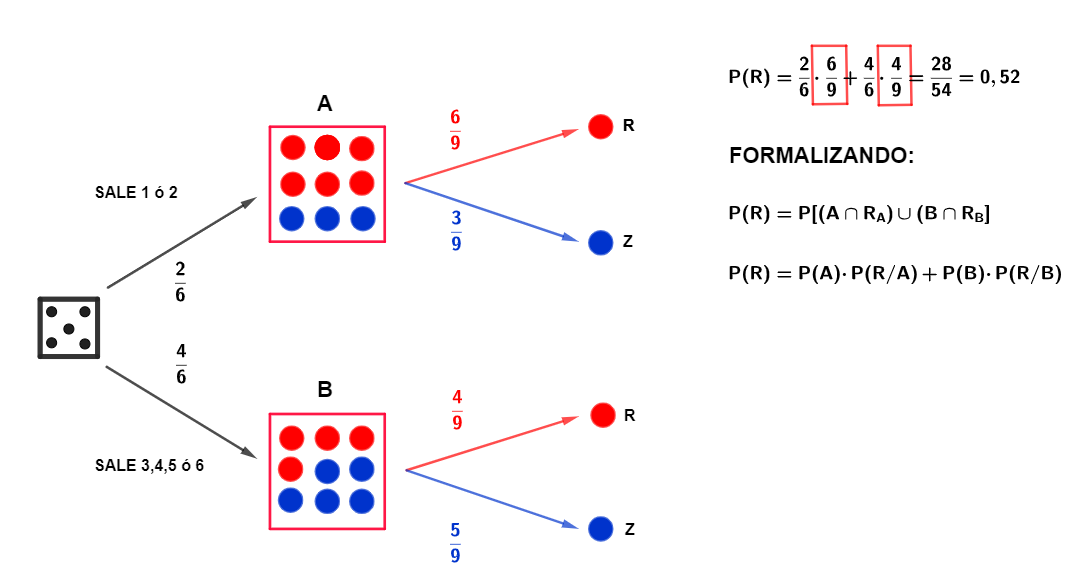
Probabilidades
En la forma anterior de resolver el ejemplo nos encontramos con el problema de que tenemos que construir el árbol completo, aunque hay ramas que no se utilicen. Por eso, en algunas ocasiones, es más rápido hacerlo directamente a través de las probabilidades.
Trabajaríamos de la siguiente forma:
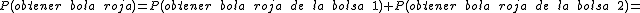
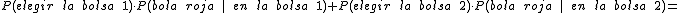
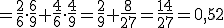
Como puedes observar las operaciones que se realizan son las mismas que hemos visto al utilizar el diagrama de árbol.
Importante
Supongamos un suceso B que depende de varios sucesos A1, A2 y A3, que tienen la característica de que abarcan todas las posibilidades de un experimento aleatorio. Para hallar la probabilidad del suceso B utilizamos la siguiente fórmula.
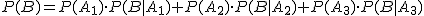
Este resultado se conoce como el Teorema de la probabilidad total. Puede ampliarse a cualquier conjunto de sucesos Ai siempre que esos sucesos sean incompatibles y juntos reúnan todos los resultados del experimento.
Caso práctico
En un bolsillo tenemos 5 monedas de un euro y 4 de dos euros. Sacamos dos monedas al azar. ¿Cuál es probabilidad de que hayamos sacado en total 3 euros?
Caso práctico
Realiza el ejercicio de probabilidad total que te plantea este enlace, alojado en proyectodescartes.org.
Comprueba lo aprendido
En una fábrica tenemos dos cajas de tornillos, en la primera son defectuosos el 5% de los tornillos mientras que en la segunda lo son el 3%. Elegimos una de las cajas al azar y extraemos un tornillo, también aleatoriamente.
Comprueba lo aprendido
|
Para practicar La siguiente escena, alojada en proyectodescartes.org, y elaborada por María José García Cebrian muestra un ejercicio de ruletas, según el color que salga en la primera elegimos una ruleta distinta y queremos saber la probabilidad de obtener pares de valores. Ten presente que la suma de todas las probabilidades debe valor 1, como ya vimos en el tema anterior. |