Resumen

Una Variable Estadística Bidimensional (X,Y) es el resultado del estudio de dos factores X e Y en los elementos de una población.

Para cada elemento de estudio obtenemos un par de valores que notaremos (x_i,y_i), donde x_i es el valor para el factor X, e y_i para el factor Y.

Por ejemplo, de una zona olivarera podemos estudiar la producción de aceite (X), y el indice de precipitaciones de un mismo año agrícola (Y). Si en dicha zona la producción de aceite de oliva de 2001 fue de 80.000 toneladas, y ese mismo año el índice de precipitaciones fue de 450 mm, tendríamos el par (80.000, 450).

A partir de la tabla de doble entrada

podemos crear las siguientes tablas de valores de las variables x e y.

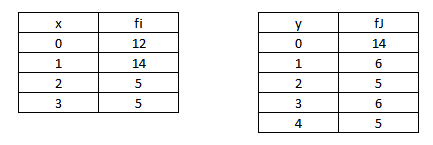
A la tabla correspondiente a la variable x se le llama distribución marginal de frecuencias absolutas de la variable x, y se ha creado tomando los valores de la variable x y los de la columna fi que figura a la derecha de la tabla de doble entrada.

A la tabla correspondiente a la variable y se le llama distribución marginal de frecuencias absolutas de la variable y, y se ha creado tomando los valores de la variable y y los de la fila fj que figura en la parte inferior de la tabla de doble entrada.

Análogamente se definen las distribuciones marginales de frecuencias relativas de la variable x y las distribuciones marginales de frecuencias relativas de la variable y.

De las tablas de arriba podemos hallar las medias y desviaciones típicas de cada una de las variables x e y, en este caso a estos parámetros se les llama media marginal y desviación típica marginal.

De la tabla de doble entrada de arriba podemos crear las siguientes tablas:

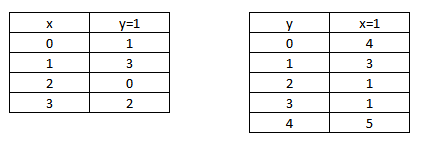
A la tabla de la derecha se le llama distribución de frecuencias absolutas de la variable x condicionada a que y=1, y se ha creado tomando los valores de la variable x y los de la columna que figura en la tabla de doble entrada.

A la tabla correspondiente a la variable y se le llama distribución de frecuencias absolutas de la variable y condicionada a que x=1, y se ha creado tomando los valores de la variable y y los de la fila que figura en la la tabla de doble entrada.

Análogamente se definen las distribuciones de frecuencias relativas de la variable x condicionada a que y=1 y las distribuciones de frecuencias relativas de la variable y condicionada a que x=1 .

En general a la variable x condicionada a que y tome un valor cualquiera se la denota como y a la variable y condicionada a que x tome un valor cualquiera se la denota como .

Para representar una distribución bidimensional podemos utilizar los siguientes gráficos:

Histograma tridimensional

Para representar la información partimos de tres ejes cartesianos. En los ejes X e Y marcamos los posibles valores de cada variable.

La altura de cada cuadrado será la correspondiente frecuencia de ese par de valores.

Diagrama de dispersión o de Burbujas

En este caso partimos de un par de ejes cartesianos X e Y en los que representamos los valores de ambos parámetros. En lugar de puntos, representamos circunferencias en las que su superficie es proporcional a la frecuencia. Ojo, no son proporcionales los radios sino las superficies. Los pares de datos que tienen frecuencia 0 no se representan.

Diagrama de dispersión o nube de puntos

Al igual que el Diagrama de Burbujas, se representa sobre un par de ejes cartesianos. En este caso, cada punto representa un par de datos de la Variable Estadística Bidimensional.