2. Tablas de doble entrada
Como has visto en el apartado anterior, tan sólo con unos cuantos datos ya se pueden establecer relaciones entre dos variables. Pero lo normal para obtener resultados fiables es contar con una gran cantidad de datos estadísticos. En estos casos no es cómodo hacer una tabla simple como las que hemos utilizado en los últimos ejemplos, en los que sólo había seis o siete datos. Vamos a ver cómo organizar la información en una tabla de doble entrada cuando tenemos muchos pares de datos.
En la siguiente presentación verás con un ejemplo cómo se crean estas tablas.
Caso práctico
Vamos a trabajar con la tabla del ejemplo anterior para sacar algunas conclusiones. Recuerda que X="número de días por mes en los que se supera el límite permitido de concentración de NO2", e Y="número de días por mes en los que se supera el límite permitido de concentración de ozono".
a) ¿Cuántos meses tuvieron 2 días con niveles excesivos de NO2 pero ninguno con nivel excesivo de ozono?
b) ¿Cuántos meses tuvieron sólo un día de exceso de concentración de NO2 en aire?
Comprueba lo aprendido
En una de las estaciones meteorológicas del Alto Guadalquivir se han recogido medidas de temperatura media (ºC) y precipitaciones medias (l/m2) cada mes. Los datos de los años 2007 y 2008 son los siguientes:
El primer par significa que en Enero de 2007 la media de temperatura fue de 7,5ºC y la media de precipitaciones fue de 7,7 l/m2.
Con estos datos, completa la tabla de doble entrada en la que las variables son X = "Temperatura media mensual" e Y = "Precipitaciones medias mensuales". Fíjate que en este caso las variables se han agrupado por intervalos. En la primera casilla tendrás que contar el número de meses en los que la temperatura media está entre 0 y 10 grados, y las precipitaciones entre 0 y 30 l/m2, que son los pares (7,5 ; 7,7) y (7,5 ; 6,1), por lo que en esa casilla pondremos un 2.
Importante
De la tabla de doble entrada del ejercicio resuelto de arriba podemos crear las siguientes tablas de valores de las variables x e y.
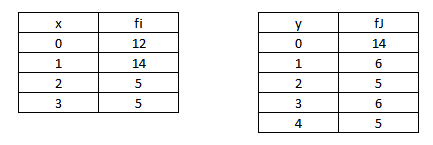
A la tabla correspondiente a la variable x se le llama distribución marginal de frecuencias absolutas de la variable x, y se ha creado tomando los valores de la variable x y los de la columna fi que figura a la derecha de la tabla de doble entrada.
A la tabla correspondiente a la variable y se le llama distribución marginal de frecuencias absolutas de la variable y, y se ha creado tomando los valores de la variable y y los de la fila fj que figura en la parte inferior de la tabla de doble entrada.
Análogamente se definen las distribuciones marginales de frecuencias relativas de la variable x y las distribuciones marginales de frecuencias relativas de la variable y.
De las tablas de arriba podemos hallar las medias y desviaciones típicas de cada una de las variables x e y, en este caso a estos parámetros se les llama media marginal y desviación típica marginal.
Importante
De la tabla de doble entrada de arriba podemos crear las siguientes tablas:
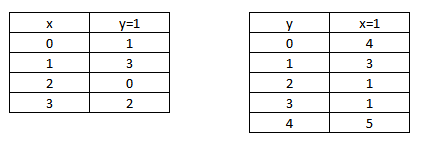
A la tabla de la derecha se le llama distribución de frecuencias absolutas de la variable x condicionada a que y=1, y se ha creado tomando los valores de la variable x y los de la columna 
que figura en la tabla de doble entrada.
A la tabla correspondiente a la variable y se le llama distribución de frecuencias absolutas de la variable y condicionada a que x=1, y se ha creado tomando los valores de la variable y y los de la fila 
que figura en la la tabla de doble entrada.
Análogamente se definen las distribuciones de frecuencias relativas de la variable x condicionada a que y=1 y las distribuciones de frecuencias relativas de la variable y condicionada a que x=1 .
En general a la variable x condicionada a que y tome un valor cualquiera se la denota como 
y a la variable y condicionada a que x tome un valor cualquiera se la denota como 
.
Caso práctico
Las calificaciones obtenidas por un grupo de alumnos en Biología y Física son:
| Biología | 3 | 4 | 6 | 7 | 5 | 8 | 7 | 3 | 5 | 4 | 8 | 5 | 5 | 8 | 8 | 8 | 5 |
| Física | 5 | 5 | 8 | 7 | 7 | 9 | 10 | 4 | 7 | 4 | 10 | 5 | 7 | 9 | 10 | 5 | 7 |
Se pide:
- Escribir la tabla de doble entrada de frecuencias absolutas.
- Hallar las distribuciones marginales así como la media y la desviación típica de las mismas.
- Hallar la distribución de la variable "calificaciones de Biología" condicionada a que la calificación de Física haya sido un 5. Y la distribución de la variable "calificaciones de Física" condicionada a que la calificación de Biología haya sido un 5.
Curiosidad
Si quieres ver los datos reales que toman estas estaciones de medición u otras estadísticas sobre Medio Ambiente, Población, Turismo, Comercio y muchas más en Andalucía, accede en el siguiente enlace al Instituto de Estadística y Cartografía de Andalucía.