2.1 Ortogonal
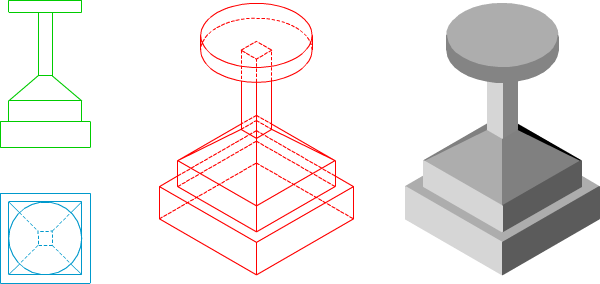
Antes de desarrollar lo contenidos de este apartado vamos a repasar los fundamentos y elementos de la axonometría ortogonal:
Las diferentes posiciones que el triedro trirrectángulo adopta respecto del plano del cuadro (ángulos de pendientes) originan tres tipos de perspectivas axonométricas ortogonales: isométricas, dimétricas y trimétricas.
Importante
Nosotros emplearemos la perspectiva Isométrica para representar figuras planas y sólidos.
Como vimos en el apartado anterior el coeficiente de reducción para cada uno de los ejes depende del ángulo que forme cada eje con el plano del cuadro. Considerando que la amplitud de dicho ángulo puede ser distinto para cada eje, tenderemos varios coeficientes de reducción.
En la siguiente tabla tienes los coeficientes de reducción empleados con más frecuencia:
| VALORES AXONOMÉTRICOS MÁS USUALES | |||||||
| Sistema | Escalas |
Coeficientes de Reducción |
Ángulos entre ejes | ||||
| X | Y | Z | XOY | XOZ | ZOY | ||
| Isométrico | 1 : 1: 1 | 0,816 | 0,816 | 0,816 | 120º | 120º | 120º |
| Dimétrico | 1: 1/2 : 1 | 0,942 | 0,471 | 0,942 | 131º 25' | 97º 10' | 131º 25' |
| 1: 1/3 : 1 | 0,973 | 0,324 | 0,973 | 133º 24' | 93º 12' | 133º 24' | |
| 1: 2/3 : 1 | 0,904 | 0,603 | 0,904 | 128º 35' | 102º 50' | 128º 35' | |
| 1: 3/4 : 1 | 0,883 | 0,662 | 0,883 | 126º 50' | 106º 20' | 126º 50' | |
| Trimétrico | 1: 1/2 7/8 | 0,872 | 0,498 | 0,996 | 168º 18' | 92º 51' | 98º 51' |
| 1: 1/2 9/10 | 0,985 | 0,493 | 0,887 | 157º | 95º 11' | 107º 49' | |
| 1: 1/2 15/16 | 0,92 | 0,644 | 0,862 | 135º | 105º | 120º | |
| 1: 1/3 23/24 | 0,951 | 0,331 | 0,993 | 157º 28' | 92º 16' | 110º 16' | |
Importante
- PERSPECTIVA AXONOMÉTRICA: se aplica coeficiente de reducción.
- DIBUJO AXONOMÉTRICO: no se aplica coeficiente de reducción.
CUADRADO AXONOMÉTRICO
Para saber más
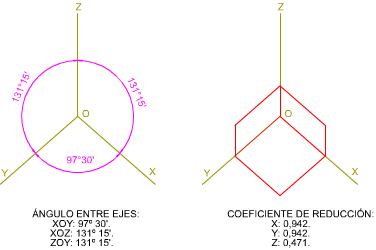
Para facilitar el trazado en la axonometría dimétrica el ángulo desigual lo forman los ejes X e Y.
Así pues, el coeficiente de reducción es igual a los dos ejes, siendo distinto para el eje Z.
En la imagen superior tienes un ejemplo de cómo se disponen los ejes en la axonometría dimétrica, la perspectiva del cuadrado queda representada como un rombo en el plano XOY y como un romboide en los planos XOZ y ZOY.
Curiosidad

Representación axonométrica
Imagen en Banco de imágenes y sonidos del Ministerio de Educación Licencia CC
Las axonometrías ortogonales se emplean, preferentemente, para representar piezas industriales, en otras ocasiones, se usan para proyectar diseños arquitectónicos, como el que aparece en la imagen superior.
Desde hace unos años las axonometrías ortogonales, sobre todo la dimétrica, se emplean en el ámbito de los videojuegos ya que permite representar la realidad virtual desde un punto de vista bastante alto (casi a vista de pájaro). En la cabecera de este tema tienes un buen ejemplo, el videojuego Goodgame Empire.
Comprueba lo aprendido
Retroalimentación
Falso
Es distinto para cada eje, solamente la Isométrica tiene el mismo coeficiente de reducción en los tres ejes.