Para calcular la superficie de una habitación cuadrada cuyos lados miden 3 metros, elevamos al cuadrado y obtenemos que el área es $A=3^2=9m^2$, pero si sabemos que el área es $9 m^2$ y queremos saber cuanto mide cada lado, tendremos que buscar el número que al elevarlo al cuadrado sea 9, que es 3. Diremos que 3 es la raíz cuadrada de 9.

En el caso anterior hemos obtenido un número entero, pero si el área mide 2, no hay ningún número racional cuyo cuadrado sea 2. Ese número es irracional y lo escribimos $\sqrt{2}=1.41421...$, tiene infinitos decimales y no es periódico. Es la raíz cuadrada de 2.

Si la piscina tiene 2 metros de lado y 2 metros de profundidad, el volumen de la piscina es $V=2^3=8m^3$ , pero si sabemos que el volumen es $8m^3$ ¿Cuánto mide cada lado? Ahora tenemos que buscar el número que elevado a 3 es 8. Ese número es 2. Decimos que 2 es la raíz cúbica de 8 y escribimos $\sqrt[3]{8}=2$. Si el volumen es $5m^3$ los lados medirán  $\sqrt[3]{5}=1.709975...$, que tiene infinitos decimales y no es periódico, luego es irracional.

Podemos utilizar las propiedades de las raíces para simplificar los cálculos y algunas expresiones en las que aparecen las raíces:

1.   $\Large\sqrt[n]{\sqrt[m]{x}}=\sqrt[n·m]{x}$
   
   
2.   $\Large\sqrt[n]{x}·\sqrt[n]{y}=\sqrt[n]{x·y}$ 
   
   
3.   $\Large\frac{\sqrt[n]{x}}{\sqrt[n]{y}}=\sqrt[n]{\frac{x}{y}}$ 
   
   
4.   $\left(\Large\sqrt[n]{x}\right)^m=\Large\sqrt[n]{x^m}$  

Ejemplos:

1.    $\sqrt[3]{\sqrt{64}}=\sqrt[3·2]{64}=\sqrt[6]{64}=2$
   
   
2.    $\sqrt[3]{2}·\sqrt[3]{4}=\sqrt[3]{2·4}=\sqrt[3]{8}=2$ 
   
   
3.    $\dfrac{\sqrt{8}}{\sqrt{2}}=\sqrt{\dfrac{8}{2}}=\sqrt{4}=2$ 
   
   
4.    $\left(\sqrt[3]{2}\right)^3=\sqrt[3]{2^3}=2$  

En los siguientes apartados utilizaremos estas propiedades con frecuencia.

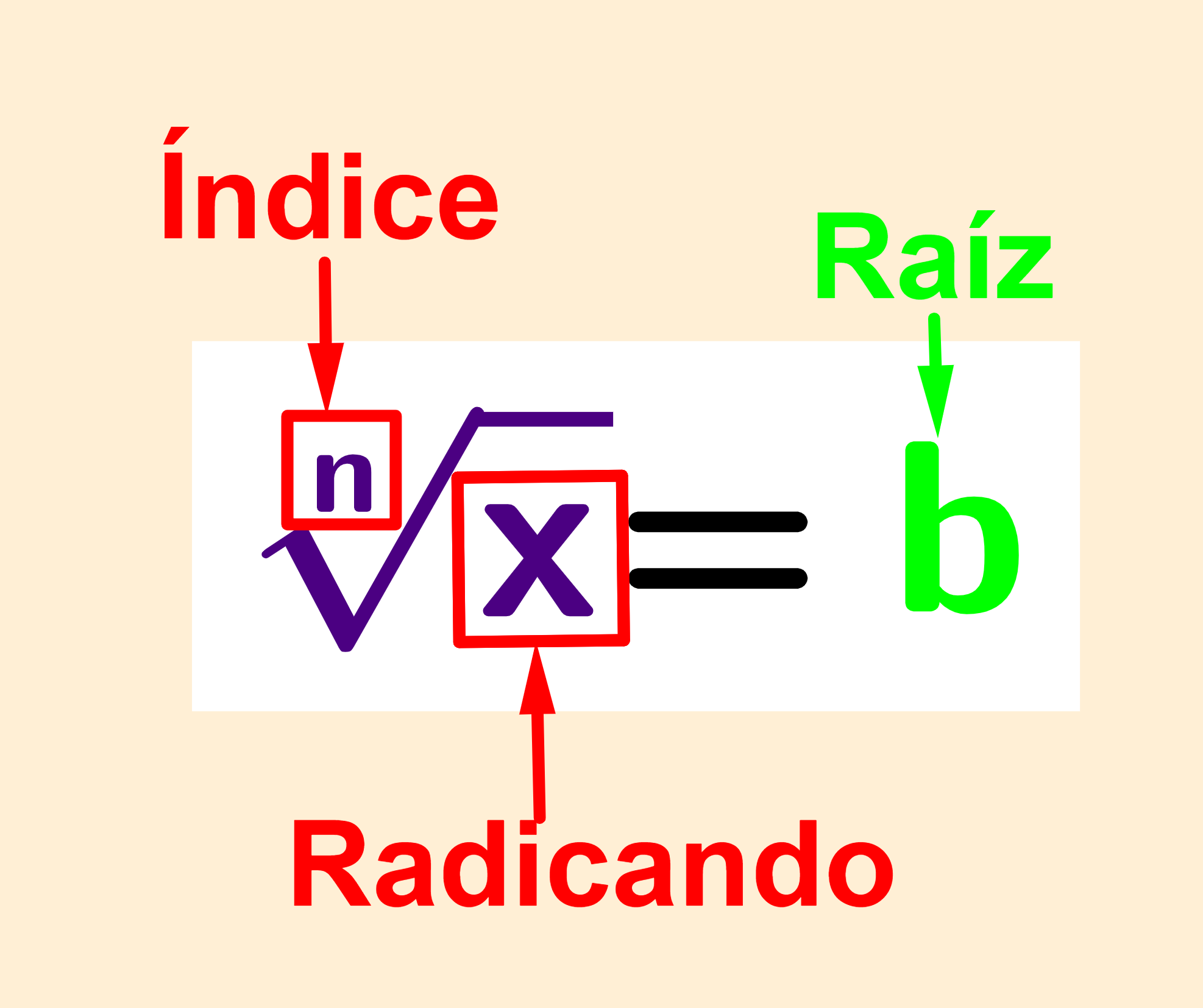
Sumas y restas

Podemos sumar los radicales que tienen el mismo índice y el mismo radicando sumando sus coeficientes. Por ejemplo $3\sqrt{x} +2\sqrt{x} =5\sqrt{x}$

Productos y divisiones

Para multiplicar dos radicales con el mismo índice sólo tenemos que aplicar la propiedad 2 que vimos anteriormente, $\sqrt[n]{x}·\sqrt[n]{y}=\sqrt[n]{x·y}$ . Por ejemplo, $\sqrt[3]{2}·\sqrt[3]{3}=\sqrt[3]{6}$ 

Para dividir dos radicales con el mismo índice aplicamos la propiedad 3, $\Large\frac{\sqrt[n]{x}}{\sqrt[n]{y}}=\sqrt[n]{\frac{x}{y}}$. Por ejemplo, $\Large\frac{\sqrt[3]{4}}{\sqrt[3]{2}}=\sqrt[3]{\frac{4}{2}}$$=\sqrt[3]{2}$ 

Si los radicales no tienen el mismo índice, debemos escribir radicales equivalentes con el mismo índice calculando el mínimo común múltiplo de los índices. Por ejemplo, para calcular $\sqrt[3]{2}\sqrt{2}$, como m.c.m(2,3)=6 y $\sqrt[3]{2}=\sqrt[6]{2^2}$ y $\sqrt{2}=\sqrt[6]{2^3}$, podemos escribir $\sqrt[3]{2}\sqrt{2}=\sqrt[6]{2^2}\sqrt[6]{2^3}=\sqrt[6]{2^2·2^3}=\sqrt[6]{2^5}$.

Lo mismo ocurre con las divisiones. Si los radicales no tienen el mismo índice debemos buscar el m.cm. Por ejemplo, $\Large\frac{\sqrt[6]{5}}{\sqrt[4]{5^3}}=\frac{\sqrt[12]{5^2}}{\sqrt[12]{5^9}}$$=\sqrt[12]{5^{2-9}}=\sqrt[12]{5^{-7}}$

Potencias

Para calcular potencias de radicales sólo hay que utilizar la propiedad 4, $\left(\sqrt[n]{x}\right)^m=\Large\sqrt[n]{x^m}$.Por ejemplo,   $\left(\sqrt{3}\right)^3=\sqrt{3^3}$. 

Racionalización

En ocasiones, tenemos fracciones con radicales en el denominador. Racionalizar es buscar una fracción equivalente en la que no aparezcan radicales en el denominador. Así, si tenemos $\Large\frac{2}{\sqrt{2}}$, buscamos una fracción equivalente en la que no aparezca $\sqrt{2}$ en el denominador. Para obtener fracciones equivalentes, recuerda que debemos multiplicar el numerador y el denominador por el mismo número. Si multiplicamos por $\sqrt{2}$, la raíz desaparecerá del denominador. Veámoslo:

$\Large\frac{2}{\sqrt{2}}=\frac{2\sqrt{2}}{\sqrt{2}\sqrt{2}}=\frac{2\sqrt{2}}{\sqrt{2^2}}=\frac{2\sqrt{2}}{2}$$=\sqrt{2}$

Si en el denominador tenemos  $\sqrt[n]{x^a}$, tendremos que multiplicar por $\sqrt[n]{x^{n-a}}$. Por ejemplo, para racionalizar $\Large\frac{7}{\sqrt[5]{2^3}}$ multiplicamos numerador y denominador por $\Large\frac{7}{\sqrt[5]{2^2}}$ y obtenemos $\Large\frac{7}{\sqrt[5]{2^3}}=\frac{7\sqrt[5]{2^2}}{\sqrt[5]{2^3}\sqrt[5]{2^2}}=\frac{7\sqrt[5]{2^2}}{\sqrt[5]{2^5}}=\frac{7\sqrt[5]{2^2}}{5}$.

Otro caso que se nos puede dar es que en el denominador nos aparezca una suma o una diferencia de raíces cuadradas, en estos casos multiplicaremos por el conjugado. Si en el denominador aparece $\sqrt{x}+\sqrt{y}$ multiplicaremos por $\sqrt{x}+\sqrt{y}$, y si aparece $\sqrt{x}-\sqrt{y}$ multiplicaremos por $\sqrt{x}+\sqrt{y}$.

Por ejemplo, $\Large\frac{3}{\sqrt{2}+\sqrt{3}}=\frac{3\left(\sqrt{2}-\sqrt{3}\right)}{\left(\sqrt{2}+\sqrt{3}\right)\left(\sqrt{x}-\sqrt{y}\right)}=\frac{3\left(\sqrt{2}-\sqrt{3}\right)}{2-3}=\frac{3\left(\sqrt{2}-\sqrt{3}\right)}{-1}$$=-3\left(\sqrt{2}-\sqrt{3}\right)$