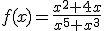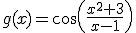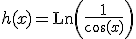3.2. Derivadas de operaciones con funciones
Actividad
| Suma | (f+g)'=f'+g' |
La derivada de la suma de funciones es la suma de las derivadas de estas funciones |
| Resta | (f-g)'=f'-g' |
La derivada de la diferencia de funciones es la diferencia de las derivadas de estas funciones |
| Producto |
(f·g)'=f'·g+g'·f |
La derivada del producto de dos funciones es igual a la derivada de la primera por la segunda sin derivar más la segunda derivada por la primera sin derivar. |
| Cociente |
La derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador sin derivar menos la derivada del denominador por el numerador sin derivar, y todo ello dividido por el denominador al cuadrado |
|
| Producto por un número | (a·f)'=a·f' |
La derivada del producto de un número real por la función es igual al número real por la derivada de la función |
| Composición |
(g°f)'=[g(f(x))]'=g'(f(x))·f'(x) |
Regla de la cadena (desarrollada más abajo) |
Veamos unos ejemplos en la siguiente presentación
La mejor forma de aprender a derivar es derivando, así que aquí tienes unos videos del Profesor de la Escuela Técnica Superior de Ingeniería Juan Medina Molina (juanmemol). Quizás sea una buena idea que pinches para verlos en pantalla completa, o pinchando sobre ellos para verlos en la página de youtube:
| Derivada de un monomio |
Derivada de una exponencial | Derivada de un polinomio |
Derivada de un producto |
|
Derivada de un monomio
Vídeo alojado en Youtube
|
Derivada
Vídeo alojado en Youtube
|
Derivada de un polinomio
Vídeo alojado en Youtube
|
Derivada - Producto de polinomios
Vídeo alojado en Youtube
|
| Derivada de un cociente | Derivada de una composición |
||
|
Derivada - Cociente de polinomios
Vídeo alojado en Youtube
|
Derivada - Potencia de cociente de polinomios
Vídeo alojado en Youtube
|
Derivada - Seno
Vídeo alojado en Youtube
|
Derivada (Coseno al cuadrado)
Vídeo alojado en Youtube
|
Importante
|
Derivada: regla de la cadena. Mariano Real.
Vídeo alojado en Youtube
|
Normalmente, las funciones que solemos encontrarnos no son funciones simples como las que vemos en la tabla de derivadas, sino que son funciones que se obtienen como composición de funciones simples.
Por ejemplo 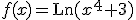 , en este caso vamos a aplicar lo que se conoce con el nombre de regla de la cadena.
, en este caso vamos a aplicar lo que se conoce con el nombre de regla de la cadena.
Si llamamos 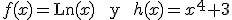 tenemos que
tenemos que 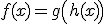
La regla de la cadena nos dice que la derivada de una función compuesta es
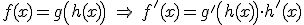 |
En nuestro caso
Ponemos a tu disposición dos tablas de derivadas tabla 1, tabla 2. Ambas recogen tanto la derivación de las funciones elementales como las compuestas. Utiliza la que te resulte más cómoda.
Una aplicación de la regla de la cadena para las funciones trigonométricas la observamos en el siguiente vídeo:
Ejemplo o ejercicio resuelto
Calcule f '(1) sabiendo que ![]()
Ejemplo o ejercicio resuelto
Calcule f '(1) sabiendo que ![]() .
.
Reflexión
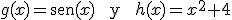 Calcula la derivada de la suma y el producto de ambas.
Calcula la derivada de la suma y el producto de ambas.
Ejemplo o ejercicio resuelto
 |
JUNIO 2011 ANDALUCÍA
Calcule la derivada de:
![]()
Ejercicio valorado en 1 punto
Reflexión
Ahora te toca practicar a tí. Para ello te proponemos que calcules la derivada de cada una de las siguientes funciones:
Caso de estudio
Aplica la regla de la cadena para obtener la función derivada de 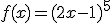
En el siguiente enlace puedes encontrar una relación de ejercicios de derivadas resueltos con los cuales puedes practicar.