2.3. Interpretación geométrica de la derivada
La derivada de una función en un punto tiene una interpretación geométrica. Observa la siguiente ventana e interactúa con ella moviendo los puntos A y B. Si dejas fijo el B y vas acercando el A a este punto, podrás comprobar que la pendiente de la recta tangente (en color verde) a la gráfica de la función se va aproximando a la de la secante (en azul). Por tanto, las ecuaciones de ambas rectas se van haciendo cada vez más semejantes ya que geométricamente ambas se van acercando.
Cuando coinciden prácticamente los puntos A y B, ambas rectas son la misma, de ahí que la derivada de la función en el punto B coincide con la pendiente de la recta tangente a la gráfica en dicho punto.
Importante
Si tenemos una función f(x), la derivada de la función en x=a, es la pendiente de la recta tangente a f(x) en el punto de abscisa x=a.
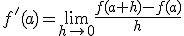 |
De esta forma, si tenemos una función f(x), su función derivada f'(x) es la función que en cada punto toma el valor de la pendiente de la recta tangente a f(x) en ese punto.
El siguiente vídeo te explica gráficamente este hecho:
Por tanto, la recta tangente a la función en el punto ![]() es:
es:
A la recta perpendicular a esta recta tangente en el punto  se le llama recta normal. Así, la ecuación de la recta normal es:
se le llama recta normal. Así, la ecuación de la recta normal es:
Hemos aplicado que la pendiente de una recta, m, y la de una recta perpendicular a ella, m', verifican que m·m'=-1.
En la siguiente escena de GeoGebra está representada en rojo la gráfica de la función y=sen(x) y en verde, la recta tangente a la gráfica de y=sen(x) en el punto A.Vemos también que la longitud del cateto opuesto del triángulo fijo en el punto A, nos da la pendiente de la recta tangente.
Si mueves con el cursor del ratón el punto A podrás apreciar cómo va desplazándose la tangente por la gráfica de y=sen(x). Su ecuación, que figura en la parte superior izquierda, va cambiando de forma continua cuando mueves el punto A.
Puedes observar cómo cambia la pendiente de la recta tangente y a su vez va surgiendo una gráfica en azul, la cual se trata de la representación de la función derivada de y=sen(x), en la parte superior derecha se va indicando en todo momento el valor de esta función para cada punto del dominio de y=sen(x), y se puede comprobar que el valor de la función derivada en todo momento coincide con el valor de la pendiente de la recta tangente cuando se desplaza esta.
Actividad de rellenar huecos
Caso de estudio
Caso de estudio
Dada la función
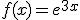
|
-
Calcula la ecuación de la recta tangente en un punto
 .
.
-
Calcula el valor de
 para que dicha recta pase por el punto
para que dicha recta pase por el punto 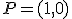
Caso de estudio
 |
|
Fotografía en Flick de Luz Adriana Villa A bajo CC
|
En la construcción de una carretera, uno de los puntos con los que hay que tener especial cuidado es en las curvas. Dependiendo de lo cerrada que sea la curva, debe tener más peralte o menos para evitar que los coches se salgan de la misma. En la construcción de una carretera, una de las curvas se adapta perfectamente a la función ![]() . Los técnicos desean tener una función que les proporcione en cada uno de los puntos de la curva la pendiente que tendrá la recta tangente a la misma. ¿Puedes ayudarles?
. Los técnicos desean tener una función que les proporcione en cada uno de los puntos de la curva la pendiente que tendrá la recta tangente a la misma. ¿Puedes ayudarles?