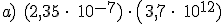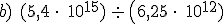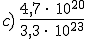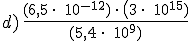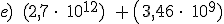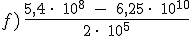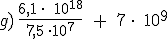4.1 Operaciones en notación científica
¿Te imaginas que tuvieras que resolver la siguiente multiplicación?
235.000.000.000.000.000.000.000 x 643.000.000.000.000.000.000.000.000
 |
|
www.actiludis.com Bajo licencia de creativee commons |
Te pasarías un buen rato escribiendo ceros! O si intentaras hacerla con la calculadora te darías cuenta de que no te caben todas las cifras. Vamos entonces a utilizar lo que hemos aprendido en los apartados anteriores para convertir una operación tan larga en otra mucho más sencilla, para ello basta con escribir estas cifras en notación científica:
(2,35 · 1023) · (6,43 · 1026)
Actividad
Vamos a explicar las operaciones a partir del ejemplo anterior:
PRODUCTO
Se multiplican las mantisas (los números decimales) y se suman los exponentes de las potencias de 10. ¡OJo! Luego se expresa el resultado como notación científica. Ejemplo:
(2,35 · 1023) · (6,43 · 1026) = (2,35 · 6,43) · (1023 · 1026) = 15,1105 · 1049
= 1,51105 · 1050
COCIENTE
Exactamente igual que el producto pero dividiendo las mantisas y restando las potencias de 10. Por ejemplo:
(2,35 · 1023) : (6,43 · 1026) = (2,35 : 6,43) · (1023 : 1026) = 0,36547 · 10-3
= 3,6547 · 10-4
SUMA Y RESTA
Primero convertimos a una misma potencia de 10, luego sumamos o restamos y por último, convertimos el resultado de nuevo a notación científica:
(2,35 · 1023) + (6,43 · 1026) = (2,35 · 1023) + (6,43 · 103·1023)=(2,35 + 643 · 103) · 1023 = (2,35 + 6430) · 1023
= 6432,35 · 1023 = 6,43235 · 1026
(2,35 · 1023) - (6,43 · 1026) = (2,35 - 6,43 · 103) · 1023 = (2,35 - 6430) · 1023
= - 6427,65 · 1023 = - 6,42765 · 1026
Para sumar y restar hay que sacar factor común la potencia de 10 cuyo exponente (en valor absoluto) sea más pequeño.
Caso de estudio
Resuelve las siguientes operaciones en notación científica y expresa el resultado en notación científica: