3. Potencia de exponente fraccionario
Caso de estudio
| fuente propia |
Ya me imagino que te lo veías venir. Exponente natural, exponente entero; y el siguiente, pues eso, el fraccionario, o sea, las fracciones, con lo que nos gustan, ¿verdad?. Bueno, ten un poco de paciencia que creo que esta vez te podemos sorprender, a no ser que sepas de antemano de qué estamos hablando.
Como siempre para entender mejor cómo es una potencia de exponente fraccionario, vamos a hacer algunos ejercicios.
Vas a necesitar la calculadora científica no solo para calcular potencias, en la cuales deberás poner entre paréntesis las potencias fraccionarias, sino para calcular raíces de índice distinto de 2. Esto lo vimos en el apartado 4 del tema 1, más concretamente donde explicamos las raíces.
Vamos a allá. Si tienes dudas sobre cómo manejar la calculadora, echa un vistazo al apartado 5.
Resuelve con la calculadora:
a.1) 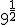 ; a.2)
; a.2) 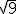
b.1) 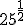 ; b.2)
; b.2) 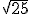
c.1) 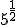 ; c.2)
; c.2) 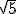
d.1) 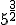 ; d.2)
; d.2) 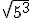
supongo que intuyes de que estamos hablando. Concrétalo en un expresión, y pincha en Mostrar información
Veamos si sigue ocurriendo cuando el índice no es 2. Calcula ahora:
a.1) 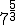 ; a.2)
; a.2) 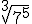 ;
;
b.1) 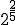 ; b.2)
; b.2) 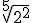
sigues obteniendo los mismos resultados ¿verdad?, de manera que intenta concluir con la generalización en letras de la potencia de un número fraccionario, y pincha después.
Propiedades de las potencias de exponente fraccionario
Las potencias de exponente fraccionario heredan las mismas propiedades que las vistas en los apartados anteriores. Además añaden la que acabamos de deducir:
|
Potencia de exponente fraccionario
|
|
Pregunta de Elección Múltiple
Solución
Solución
Solución
Solución
Solución
Solución
Ejemplo o ejercicio resuelto
Ejercicios de repaso de las potencias:
1.- Pasa a raíz las siguientes potencias de exponente fraccionario:
a) 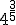 ; b)
; b) 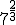 ; c)
; c) 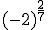 ; d)
; d) 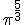 ; e)
; e) 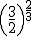
2.- Pasa a potencia de exponente fraccionario las siguientes raíces:
a) 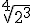 ; b)
; b) 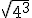 ; c)
; c) 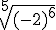 ; d)
; d) 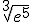 ; e)
; e) 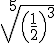
3.- Expresa estas potencias como potencia única, siempre con exponente positivo:
a)  ; b)
; b) 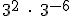 ; c)
; c) 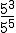
4.- Expresa en forma de potencia única las siguientes potencias, y calcula el resultado:
a) 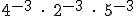 ; b)
; b) 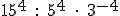 ; c)
; c) 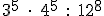 ; d)
; d)