1. Potencia de exponente natural
| |
|
http://lewebpedagogique.com/hispadictos/tag/restaurante/ |
Un amigo me asaltó el otro día con una duda matemática. Me dijo que había estado en un restaurante que tenía un menú variado. Le ofrecían primer y segundo plato, y postre. Además, había 4 primeros platos, 4 segundos y 4 postres.
Lo mejor para mi amigo era que podía comer en el mismo restaurante sin repetir el mismo menú durante mucho tiempo. Como a él las cuentas se le dan mal, me preguntó, ¿y cuántos días puedo estar comiendo sin repetir el mismo menú?
Fácil le contesté. Tienes 4 posibilidades para el primero. Para cada una de esas posibilidades tienes 4 para el segundo, o sea, 4 posibilidades para la opción 1, 4 para la opción 2, etc... esto nos arroja que por el momento tenemos 4·4=16 posibilidades, y para cada una de ellas un postre distinto, o sea, 16 con el postre 1, 16 con el postre 2, etc... así tenemos 16·4=64 posibilidades. O mejor dicho, 4·4·4 posibilidades. Esto lo podemos expresar así: 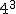
Actividad
Dado un número real a y un número natural n, llamamos potencia de base a y exponente n, al número
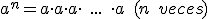
que se consigue multiplicando la base a, por sí misma tantas veces como indique el exponente n. Por ejemplo:
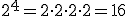 ;
; 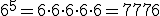 ;
; 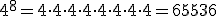
Caso de estudio
Ejercicio
Utilizando la definición anterior, y tu calculadora científica resuelve las siguiente potencias:
a) 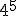 ; b)
; b) 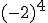 ; c)
; c) 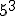 ; d)
; d) 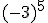 ; e)
; e) 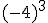 ; f)
; f) 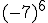
Una vez realizadas las potencias, pincha en Mostrar información para comprobarlas.
Ahora te toca a ti:
a) 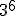 ; b)
; b) 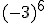 ; c)
; c) 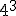 ; d)
; d) 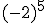 ; e)
; e) 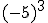 ; f)
; f) 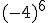
Intenta calcular las siguientes potencias que, aunque parecen iguales, hay algunas diferencias:
a)
b)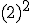
c)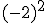
d)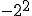
e)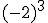
f)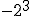
Actividad
Si observas detenidamente el ejemplo anterior podemos sacar algunas conclusiones:
- Si el signo está dentro del paréntesis, formará parte de la base y por consiguiente se repetirá tantas veces como nos indica el exponente.
- Si el signo está fuera del paréntesis, no forma parte de la base y por consiguiente se añadirá al resultado de la potencia.
- Si la base es positiva, el resultado será positivo.
- Si la base es negativa y el exponente es par, el resultado será positivo.
- Si la base es negativa y el exponente es impar, el resultado será negativo.