1.2. Yo, polinómica, y tú, racional
Apenas hemos iniciado el tema y ya has puesto en práctica una gran cantidad de conocimientos que poseías sobre las funciones y que has aplicado al ver su gráfica.
Además, hemos recogido en el cuadro-resumen del apartado anterior, un procedimiento que debes tener presente a la hora de abordar el análisis y la representación de la gráfica de cualquier función.
Este punto lo dedicaremos única y exclusivamente a abordar la representación gráfica y el estudio de las funciones polinómicas y racionales.
 |
|
Imagen de Stinging Eyes con licencia CC BY-SA 2.0 |
Actividad
Una función polinómica es aquella cuya expresión es un polinomio. Su expresión general es:
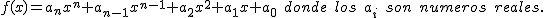
Ya has trabajado con funciones polinómicas a lo largo del curso:
+ Las funciones polinómicas de grado 1 son las funciones lineales (sus gráficas son líneas rectas)
+ Las funciones polinómicas de grado 2 son las funciones cuadráticas (sus gráficas son parábolas)
Todas las funciones polinómicas presentan una serie de características, atributos, comunes. Es normal, la genética, también juega su papel en entre las funciones miembros de una misma familia. Son las siguientes:
| Características comunes a todas las funciones polinómicas |
|
|
|
|
|
|
Ejemplo o ejercicio resuelto
A continuación vamos a efectuar la representación e interpretación de la gráfica de una función polinómica con ayuda de Geogebra para poner en práctica las características de las funciones polinómicas.
|
|
AV - Actividad de Espacios en Blanco
Caso de estudio
Para practicar más.
(a) Sitúate sobre la curva de la gráfica de la función f representada en el applet de Geogebra anterior.
Pulsa el botón derecho y selecciona Propiedades del menú desplegable que aparece.
A continuación, en el campo Valor del formulario que aparece introduce la expresión: x3 + x2 - 4x - 4
Finalmente, pulsa sobre el botón Cierra.
Hecho ésto, aparecerá la gráfica de la nueva función introducida y sus valores respectivos para Extremos, Puntos de Corte y Puntos de Inflexión.
Para terminar de ajustar la gráfica a la ventana, utiliza el Zoom cuanto necesites, pulsando el botón derecho sobre cualquier lugar vacío de la ventana. También puedes mover la misma a tu antojo e incluso los rótulos que aparecen.
Si te confundes y quieres volver a empezar, basta con que hagas click en la esquina superior derecha del applet de Geogebra, sobre el icono de reset y todo volverá a estar como al principio.
(b) Analiza la gráfica con todos los puntos indicados en el cuadro-resumen que indicamos al principio del tema.
Actividad
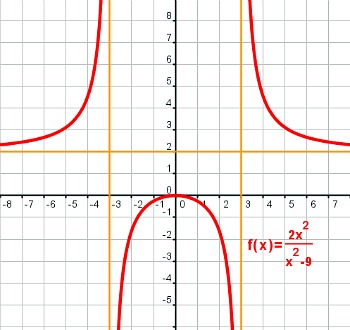
Una función es racional si es el cociente de dos polinomios. Su expresión general es:
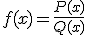
Como bien sabes, los componentes de una misma familia comparten ciertos parecidos razonables sobre todo en sus rasgos físicos, los más perceptibles a primera vista.
Pues, de igual modo que ocurre en seres vivos y que hemos visto anteriormente que sucedía con las funciones polinómicas, en el caso de las funciones racionales, su imagen, es decir, sus gráficas, también comparten ciertas características comunes. Se enumeran a continuación:
| Características comunes a todas las funciones racionales |
Dom(f) =
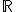 \ { \ {
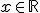 , tales que Q(x)=0} , tales que Q(x)=0}
|
|
|
|
AV - Pregunta de Selección Múltiple
Solución
Solución
Solución
Solución
Actividad de Espacios en Blanco
Pulsa en este enlace donde accederás a una ventana de Wiris y siguiendo los 3 pasos indicados en el procedimiento descrito en el vídeo anterior representa la función:
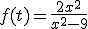
Finalmente, rellena las huecos en blanco.
Pre-conocimiento
Antes de continuar con el tema, ¿por qué no nos pegamos frente al espejo unos buenos movimientos de baile practicando con la gráfica de algunas de las funciones más conocidas? ¿Te animas?
 |