2.2 Cálculos en los que intervienen volúmenes de gases
Curiosidad
| En volumen iguales de gases diferentes, medidos a la misma presión y temperatura, hay el mismo número de moléculas |  |
| Imagen de Jorge Elías en flickr. CC |
La frase que acabas de leer es el enunciado de la ley de Avogadro que ya hemos estudiado.
Imagínate que tenemos en tres recipientes de un litro de capacidad H2, Ne y CO2. Si la temperatura y la presión es la misma en los tres recipientes, podemos afirmar que en ellos existen el mismo número de moléculas. Pero, ¿cómo es posible esto si las moléculas son diferentes y tienen distinta masa y tamaño?
El tamaño de las moléculas es despreciable comparado con la distancia entre ellas y con la capacidad del recipiente, por lo que podemos considerar que todas las moléculas se comportan igual, como si fuesen puntos.
Parece lógico pensar que cuanto mayor sea la masa molecular de una sustancia y la velocidad media de las moléculas, mayor será la presión ejercida por la misma. Pero para una misma temperatura, cuanto mayor sea la masa de las moléculas, menor es su velocidad y, por tanto, el incremento que debería producirse en la presión debido a una mayor masa, se ve compensado con la disminución que se produce en la presión al moverse las moléculas con menor velocidad.
Ya hemos visto anteriormente que 1 mol de cualquier gas ocupa en condiciones normales, es decir, a una temperatura de 0ºC y a una presión de 1 atmósfera, 22, 4 litros.
Por ejemplo, si queremos saber el volumen que ocupan 2,5 mol de metano en condiciones normales, tendremos que multiplicar 2,5 mol por el factor de conversión 22,4 L/1 mol. De esta manera, se eliminan los "moles" y aparecen los "litros":
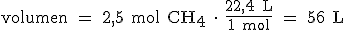
Si lo que queremos saber son los moles que hay en 100 litros de CO2 medidos en condiciones normales, el factor de conversión será en este caso, el inverso al anterior:
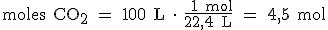
Importante
Ejemplo o ejercicio resuelto
Dada la reacción de descomposición del clorato de potasio:
2 KClO3 → 2 KCl + 3 O2
Calcula:
a) Los gramos de clorato de potasio necesarios para obtener 12 litros de oxígeno, medidos en condiciones normales.
b) Los gramos de cloruro de potasio que se obtienen a partir de 10 g de clorato de potasio.
Datos. Masas atómicas relativas: Cl = 35,5 ; K = 39 ; O = 16
La ecuación química está ajustada.
a) Escribimos lo que queremos hallar, el signo "igual" y el dato de partida:
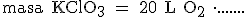
Para pasar de litros a moles de oxígeno, tenemos en cuenta que 1 mol de cualquier gas, en condiciones normales, ocupa 22,4 L:
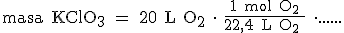
Ahora, tenemos que pasar de moles de O2 a moles de KClO3. Si te fijas en la ecuación química, por cada 2 mol de KClO3 se forman 3 mol de O2:
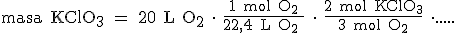
Por último, pasamos de moles a gramos teniendo en cuenta que la masa de 1 mol de KClO3 es 122,5 gramos (39+35,5+3x16):
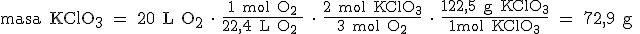
b) Tendremos que pasar de gramos de KClO3 a moles de KClO3, de moles de KClO3 a moles de KCl, y de moles de KCl a gramos de KCl:
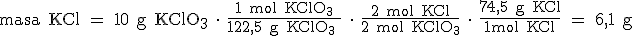
AV - Reflexión
Se hacen reaccionar 10 g de cinc metálico con ácido sulfúrico en exceso. La reacción que tiene lugar es:
Zn (s) + 2 HCl (ac) → ZnCl2 (ac) + H2 (g)
Calcula:
b) El volumen de hidrógeno que se obtiene en condiciones normales de presión y temperatura.
Datos. Masas atómicas: Cl = 35,5 u; Zn = 65,4 u.
¿Y si el gas no se encuentra en condiciones normales? En este caso, para relacionar la cantidad de sustancia de un gas (los moles) con el volumen que ocupa (los litros) tendremos que aplicar la ecuación de los gases ideales:
donde "n" es el número de moles; "P", la presión en atmósferas; "V", el volumen en litros; "T", la temperatura en kelvin; y "R", la constante de los gases que, como sabes, vale 0,082 atm.L.K-1.mol-1. De la expresión anterior se deducen estas otras:
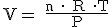 |
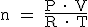 |
Importante
La ecuación de los gases ideales relaciona los moles de un gas con el volumen que ocupa a una presión y a una temperatura determinada.
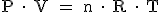
donde:
"P" es la presión en atmósferas ( 1 atm = 760 mm Hg); "V" el volumen en litros; "n", el número de moles; "T", la temperatura en kelvin ( K = ºC + 273); " y "R", la constante de los gases: 0,082 atm.L.K-1.mol-1.
Curiosidad
La ecuación de los gases ideales es una ecuación general y, por tanto, se puede utilizar también cuando la sustancia gaseosa se encuentra en condiciones normales. Si sustituimos "n" por 1 mol, "P" por 1 atm, "T" por 273 K, y despejamos V, nos saldrán 22,4 L.
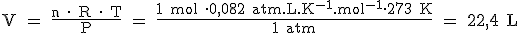
Ejemplo o ejercicio resuelto
La roca caliza, muy usada en construcción, está formada por carbonato de calcio, el cual se descompone por el calor dando lugar a óxido de calcio y dióxido de carbono:
CaCO3 → CaO + CO2
Si se descomponen por el calor 2 kg de carbonato de calcio, calcula el volumen que ocupará el dióxido de carbono obtenido, medido a 27ºC y 0,9 atm de presión.
Datos. R = 0,082 atm.L.K-1.mol-1 . Masas atómicas: C = 12 u ; O = 16 u ; Ca = 40 u
La ecuación está ajustada.
Vamos a pasar los 2000 g de CaCO3 a moles, y después, de moles de CaCO3 a moles de CO2:
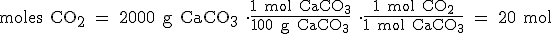
Ahora despejamos "V" de la ecuación de los gases ideales y sustituimos todos los datos:
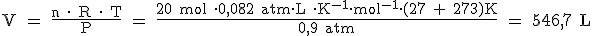
AV - Reflexión
Dada la siguiente reacción química :
Calcula:
a) Los moles de N2O5 que se obtienen a partir de 20 g de AgNO3.
b) El volumen de oxígeno obtenido, medido a 20 ºC y 620 mm de mercurio.
Datos: R = 0,082 atm.L.K-1.mol-1. Masas atómicas: N = 14 u; O = 16 u; Ag = 108 u.