2.1. Ecuaciones lineales
 |
| Fotografía en Flickr de roblz.com bajo CC |
Ecuaciones de primer grado
Empezaremos resolviendo ecuaciones con una incógnita que además no tenga exponente, es decir, de primer grado. Para ello veremos varios métodos y empezaremos por el más intuitivo: la resolución por tanteo o por aproximación.
Cuando buscamos la solución de una ecuación, lo que queremos es encontrar un número que, al sustituirlo por x, verifique la igualdad. En eso consiste la resolución por tanteo, en darle valores a la incógnita x hasta que se igualen ambos términos.
Por ejemplo, supongamos que tenemos la ecuación: 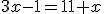 . Vamos a sustituir x por algunos valores y veamos qué pasa.
. Vamos a sustituir x por algunos valores y veamos qué pasa.
| Valores |
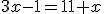 |
Observaciones |
Si 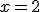
|
3 · 2 - 1 = 11 + 2 5 = 13 |
No se igualan los miembros.
Necesito aumentar el valor del primero. |
Si 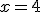 |
3 · 4 - 1 = 11 + 4 11 = 15 |
Sigue sin igualar. |
Si 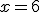
|
3 · 6 - 1 = 11 + 6 17 = 17 |
La solución de la ecuación es 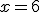
|
AV - Actividad de Espacios en Blanco
Actividad
Dos o más ecuaciones son equivalentes cuando tienen las mismas soluciones.
En la siguiente presentación vas a descubrir con todo lujo de detalles (propiedades, pasos...) cómo se resuelve una ecuación de primer grado.
| Presentación en Slideshare por Patricia_Perez |
Además, las acompañamos de unos vídeos de juanmemol de su canal ecuaciones de primer grado. Por cierto si te sabe a poco, si pinchas en este enlace descubrirás 52 vídeos más. Toda una lección de ecuaciones.
Resumiendo la presentación anterior, este método de resolución podemos simplificarlo en cuatro pasos:
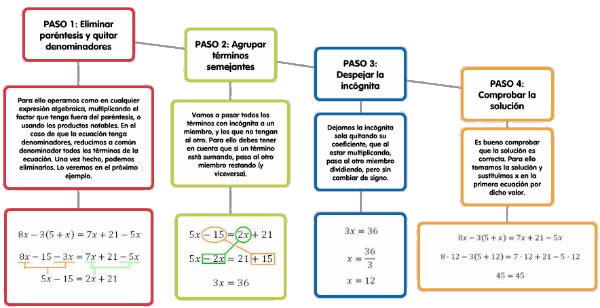
|
| Imagen de elaboración propia |
Ejemplo o ejercicio resuelto
Intenta resolver la siguiente ecuación paso a paso. Si no sabes seguir, puedes consultar el resultado.
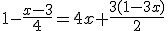
Paso 4: Despejar la incógnita
Este paso no es necesario, pues ya la tenemos despejada.
Paso 5: Comprobar la solución
Actividad
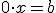 , con
, con 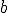 un número distinto de cero, la ecuación no tiene solución. Se dice entonces que dicha ecuación es incompatible.
un número distinto de cero, la ecuación no tiene solución. Se dice entonces que dicha ecuación es incompatible.
 |
| Fotografía en Flickr por antiuser bajo CC |
Ecuaciones de segundo grado
Una ecuación será de segundo grado si tiene algún término en 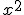 y no tiene términos de grado superior.
y no tiene términos de grado superior.
Para resolver una ecuación de segundo grado, en principio, seguimos el mismo método que para las ecuaciones de primer grado, ir buscando ecuaciones equivalentes cada vez más sencillas, hasta obtener una ecuación de la forma 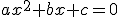 , donde
, donde  ,
, 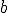 y
y  son números reales.
son números reales.
Las ecuaciones de segundo grado pueden tener dos, una, o ninguna solución. Para resolverlas, usaremos la siguiente fórmula:
Caso de estudio
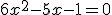
Ejemplo o ejercicio resuelto
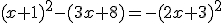
- Quitamos paréntesis:
- Pasamos todos los términos al mismo miembro:
- Usamos la fórmula de resolución:
AV - Actividad de Espacios en Blanco
Resuelve las siguientes ecuaciones y completa los huecos. Si tiene una única solución, escríbela repetida en cada hueco. Si no tiene solución, escribe no en cada hueco. Los huecos con una barra / entre ambos indican una fracción.
Número de soluciones de una ecuación de segundo grado
En la fórmula hay una raíz cuadrada que va a ser la que determine el número de soluciones de la ecuación. La expresión a la que calculamos la raíz, 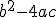 , se llama discriminante. Tendremos los siguientes casos:
, se llama discriminante. Tendremos los siguientes casos:
- Si
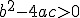 : La raíz existe, y por lo tanto la ecuación tendrá dos soluciones, una operando con el signo + y otra con el signo -.
: La raíz existe, y por lo tanto la ecuación tendrá dos soluciones, una operando con el signo + y otra con el signo -. - Si
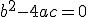 : La raíz vale 0 y la ecuación tendrá una única solución,
: La raíz vale 0 y la ecuación tendrá una única solución, 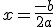 .
. - Si
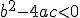 : La raíz no existe y la ecuación no tiene solución.
: La raíz no existe y la ecuación no tiene solución.
Ecuaciones de segundo grado incompletas
Importante
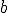 o
o  son cero.
son cero.
 |
| Imagen de elaboración propia |
Aunque para resolver las ecuaciones incompletas se puede recurrir a la fórmula general, se pueden resolver de forma más sencilla usando los siguientes métodos:
Faltael término independiente 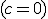 |
Falta el término en 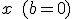 |
Si en la ecuación no aparecieran a la vez los términos 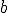 y
y  , la ecuación tendría una única solución,
, la ecuación tendría una única solución,  .
.
Caso práctico
 |
Curso 2014/2015
Resuelva la ecuación:
![]()