Resumen

Importante

Recuerda que:

Si un coeficiente multiplica a una variable, no escribimos el signo de multiplicar:
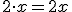
Si un coeficiente o una variable multiplica a un paréntesis, tampoco es necesario ponerlo:
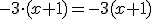
Al multiplicar variables de la misma base sumamos los exponentes:

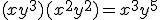
Importante

Un monomio es una expresión algebraica formada por productos de números (coeficiente) y letras (parte literal).

Cuando en un monomio interviene una sola letra, su exponente es el grado del monomio. Cuando la parte literal está formada por dos o más letras distintas el grado del monomio es la suma de los exponentes de las letras que lo forman.

Dos monomios son semejantes si tienen la misma parte literal.

La suma o resta de dos o más monomios con distinta parte literal dan como resultado un polinomio.

Importante

El valor numérico de un polinomio P(x) para el punto x = a, que se representa por P(a), es el resultado de sustituir la variable x por a y efectuar las operaciones.

Importante

Suma y resta de polinomios

Para sumar o restar polinomios, tan solo debemos operar con los monomios que tengan la misma parte literal, recordando que la parte literal es la variable con su exponente.

Multiplicación de polinomios

Al multiplicar un monomio por un polinomio, tan solo debemos aplicar la propiedad distributiva.

$3x^2\cdot(x^2-2x+5) = 3x^4-6x^3+15x^2$

Si queremnos multiplicar dos polinomios, aplicaremos reiteradamente la propiedad distribuitiva.

División de polinomios

División de monomios.
Dividimos los coeficientes y las partes literales. Ejemplo 3x⁵:2x²= $\frac{3}{2}x^3$
División de un polinomio entre un monomio.
Dividimos cada término del polinomio entre el monomio. Ejemplo (3x⁴-2x3+3x):3x =
División de un polinomio entre un polinomio.
1. Ordenamos los polinomios según las potencias y de mayor a menor.
2. Se dividen los primeros términos del dividendo y del divisor.
3. El resultado obtenido se multiplica por el divisor y se resta al dividendo.
4. Seguimos este procedimiento hasta que el resto sea de un grado menor que el divisor. Ejemplo:(3x⁴-2x³+4x²+2x-2):(x²-2x-1)

Imagen en Wikipedia. Licencia CC

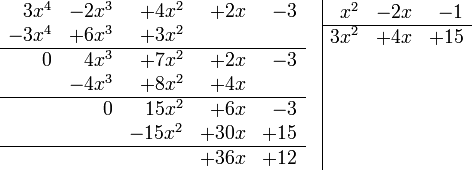
Importante

Teorema del Resto

El resto de la divisíon del polinomio P(x) y el binomio (x-a), es el valor numérico del polinomio para x=a.

Para realizar divisiones entre un polinomio P(x) y un binomio (x-a), podemos utilizar la regla de Ruffini en lugar de utilizar el métido clásico de división de polinomios.

Importante

La factorización de un polinomio es la descomposición de un polinomio en polinomios irreducibles, entendiendo irreducible como que no se puede expresar como producto de polinomios de menor grado.

Debemos calcular en primer lugar una raiz entera del polinomio para convertir el polinomio P(x) en Q(x)·(x-b). Realizando el mismo procedimiento con Q(x) y reiterando el procedimiento, llegaremos a una expresión del tipo P(x) = a(x-b)(x-c)···(x-d).

Para buscar soluciones enteras debemos buscar en los divisores del termino independiente entre el coeficiente líder.