4.3. Factorización de polinomios
Al igual que hacíamos con los números enteros, los polinomios también pueden descomponerse como producto de elementos más "pequeños"
Importante
La factorización de un polinomio es la descomposición de un polinomio en polinomios irreducibles, entendiendo irreducible como que no se puede expresar como producto de polinomios de menor grado.
Debemos calcular en primer lugar una raiz entera del polinomio para convertir el polinomio P(x) en Q(x)·(x-b). Realizando el mismo procedimiento con Q(x) y reiterando el procedimiento, llegaremos a una expresión del tipo P(x) = a(x-b)(x-c)···(x-d).
Para buscar soluciones enteras debemos buscar en los divisores del termino independiente entre el coeficiente líder.
Factoricemos el polinomio P(x) = x3 - 7x + 6. En primer lugar buscamos los divisores del término independiente, en este caso ![]() . Buscamos con la regla de Ruffini, algunas soluciones del polinomio.
. Buscamos con la regla de Ruffini, algunas soluciones del polinomio.
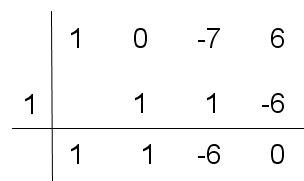
Así P(x) = x3 - 7x + 6 = (x - 1) · (x2 + x - 6)
Actuamos ahora de modo análogo con el polinomio (x2 + x - 6)
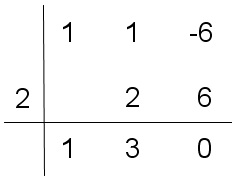
Así (x2 + x - 6) = (x - 2) · (x + 3), por lo que P(x) = (x - 1) · (x - 2) · (x + 3)
Reseñar que si buscamos una raiz mediante Ruffini y el resto no es cero, probaremos con otro.
Si todavía no te ha quedado muy claro, puedes ver otro ejemplo en el siguiente vídeo.
Vídeo de lasmatematicas.es alojado en YouTube
Ejercicio resuelto
Factoriza el polinomio x3 + x2 - 4x - 4
Comprueba lo aprendido
Comprueba lo aprendido
Retroalimentación
Verdadero
Si el polinomio que queremos descomponer es de grado 2, podremos realizar la factorización sin necesidad de utilizar la regla de Ruffini.
Vídeo de Tuto mate alojado en YouTube