4.2. Regla de Ruffini
En algunas ocasiones, no será necesario aplicar el procedimiento visto en los apartados anteriores para realizar la división de dos polinomios.
Importante
Para realizar divisiones entre un polinomio P(x) y un binomio (x-a), podemos utilizar la regla de Ruffini en lugar de utilizar el métido clásico de división de polinomios.
Veamos la división de los polinomios (x3 - 2x2 + 4) : (x - 1)
- Si el polinomio a dividir, no es completo, añadimos los términos con coeficientes 0. Pasamos de x3 - 2x2 + 4 a x3 - 2x2 + 0·x + 4
- Indicamos los coeficientes del polinomio P(x) y en un nivel inferior el opuesto del término independiente del divisor.
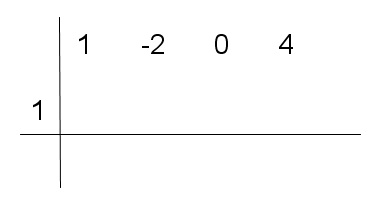
- Bajamos a la zona inferior el primer coeficiente.

- Multiplicamos el coeficiente bajado por el divisor y lo colocamos bajo el segundo coeficiente.
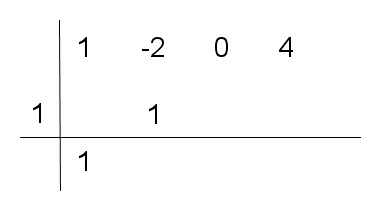
- Sumamos los términos de la segunda columna obteniendo.
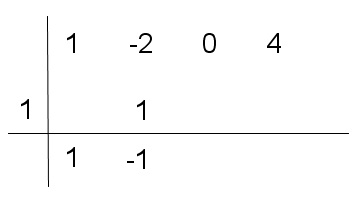
- Repetimos el procedimiento.
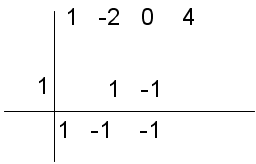
- Volvemos a aplicar el mismo proceso y llegamos al siguiente esquema.
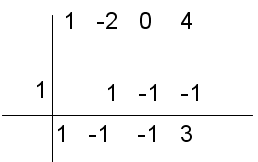
El cociente es el polinomio de un grado inferior al dividendo y cuyos coeficientes están en la última fila del esquema mostrado, es decir el cociente es 1·x2 - 1·x - 1, siendo el último número, el resto de la división, es decir: x2 - x - 1, de resto 3.
En este vídeo puedes ver una explicación muy clara de esta regla.
Vídeo de Tuto mate alojado en YouTube
Ejercicio resuelto
Realiza la división de los polinomios x2 - 4x + 1 entre x - 3 utilizando la regla de Ruffini
Ejercicio resuelto
Utiliza la regla de Ruffini para la siguiente operación (x4 - 3x3 + x2 - 2) : (x + 1)
Comprueba lo aprendido
Determina la siguiente división con el uso de la regla de Ruffini. (x4 - x + 1) : (x + 2)