2.3. Operaciones con expresiones algebraicas
Importante
Tanto en la suma como en la multiplicación de expresiones algebraicas se conservan las propiedades anteriormente vistas en los números reales (conmutativa, asociativa, distributiva...)
Suma y resta:
Fíjate en la siguiente expresión: 
Está formada por siete sumandos llamados términos. En cada término (por ejemplo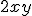 
) podemos distinguir una parte numérica o coeficiente (en nuestro caso 2) y una parte literal (
).
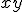Los términos que tengan exactamente la misma parte literal son términos semejantes. Esos serán los que podemos sumar y restar. En nuestro ejemplo, encontramos cuatro tipos diferentes de términos semejantes.
La suma y la resta consisten básicamente en "contar" los términos semejantes:
- Término
: 
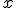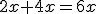
- Término
: 
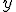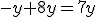(Recuerda que 
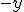equivale a 
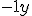) - Término
: 
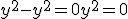
- Término :
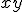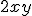
Resumiendo, 
Producto:
Para realizar el producto de un término por toda una expresión, multiplicaremos el primero por cada uno de los términos de la segunda expresión. Esto se resuelve multiplicando los coeficientes entre sí, y las variables entre sí. Por ejemplo,
Para multiplicar dos expresiones, haremos lo mismo pero multiplicando cada término de la primera expresión por cada uno de los términos de la segunda expresión. Luego sumaremos los términos semejantes para dejar el resultado lo más simplificado posible.
Importante
Recuerda que:
- Si un coeficiente multiplica a una variable, no escribimos el signo de multiplicar:
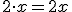
- Si un coeficiente o una variable multiplica a un paréntesis, tampoco es necesario ponerlo:
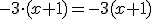
- Al multiplicar variables de la misma base sumamos los exponentes:
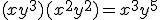
Identidades notables
Hay tres fórmulas que debes conocer. Facilitan las operaciones y te serán de gran ayuda a la hora de simplificar expresiones.
| CUADRADO DE UNA SUMA | |
| Fórmula | Ejemplo |
 Imagen de elaboración propia
|
Vídeo de las matemáticas.es alojado en Youtube
|
| CUADRADO DE UNA DIFERENCIA | |
| Fórmula | Ejemplo |
 Imagen de elaboración propia
|
Vídeo de las matemáticas.es alojado en Youtube |
| SUMA POR DIFERENCIA | |
| Fórmula | Ejemplo |
 Imagen de elaboración propia
|
Vídeo de las matemáticas.es alojado en Youtube
|