3.1 Aplicaciones
El magnetismo sobre cargas en movimiento tiene aplicaciones muy interesantes, por ejemplo, las dos que te presentamos aquí:
EL CICLOTRÓN
| Vídeo de wolframmathematica alojado en Youtube |
En el ciclotrón se combinan la acción de un campo eléctrico alterno, que les proporciona sucesivos impulsos, con un campo magnético uniforme que curva su trayectoria y las redirige una y otra vez hacia el campo eléctrico. Fue inventado en el año 1934 por los físicos estadounidenses Livingston (1905-1986) y Lawrence (1901-1958) (por este motivo, este último recibió en 1939 el premio Nobel).
En la vídeo de la derecha puedes ver el funcionamiento del ciclotrón. Observa que el dispositivo consta de dos cámaras semicirculares (llamadas "des" por su forma) que se encuentran en el interior de un campo magnético perpendicular a ellas. Ese campo magnético las obliga a describir un semicírculo antes de entrar en una zona de campo eléctrico que las acelera hasta la otra "de", donde vuelven a describir un círculo de mayor radio antes de volver a ser aceleradas por el campo eléctrico (que ahora está invertido)
La velocidad que adquieren las partículas después de cada semicircunferencia es:
![]()
No olvides que la velocidad angular correspondiente es:
![]() y la frecuencia correspondiente a esta velocidad
y la frecuencia correspondiente a esta velocidad
![]()
Ese valor debe el mismo al que tiene que oscilar el campo eléctrico para que esté sincronizado con las partículas y las acelere cada vez que pasen por la zona de campo eléctrico. Se le llama frecuencia de resonancia del ciclotrón.
ESPECTRÓMETRO DE MASAS
¿Te has preguntado alguna vez cómo es posible conocer datos de masa de partículas atómicas, siendo estas tan pequeñas? El espectrómetro de masas permite analizar la composición de diferentes elementos químicos e isótopos atómicos, separando los núcleos atómicos en función de su relación carga-masa (q/m).
Consta de una cámara donde se producen iones de cierta sustancia, los cuales son acelerados por un campo eléctrico hasta penetrar en una región en la que existe un campo magnético perpendicular que los obliga a describir círculos de cierto radio R. La idea es medir el radio experimentalmente observando el impacto de las partículas en una pantalla detectora. Como los diferentes isótopos tienen igual carga pero diferente masa, las circunferencias descritas tendrán diferentes radios, con lo que consigues encontrar su relación carga-masa. Estas son las cuentas que hay que hacer:
El radio de la semicircunferencia descrita ya lo has visto en apartados anteriores, viene dado por:
![]()
Por otra parte, la velocidad de las partículas al entrar en la zona de campo magnético se puede obtener igualando su variación de energía cinética con la disminución de energía potencial. Fíjate que esta expresión permite calcular la velocidad de los iones en función de la diferencia de potencial que se aplica, o sea, que la velocidad de las partículas se controla experimentalmente a través de la diferencia de potencial.
![]()
Combinando las dos ecuaciones nos queda la relación carga-masa:
![]()
La siguiente imagen representa el principio de funcionamiento del espectrómetro
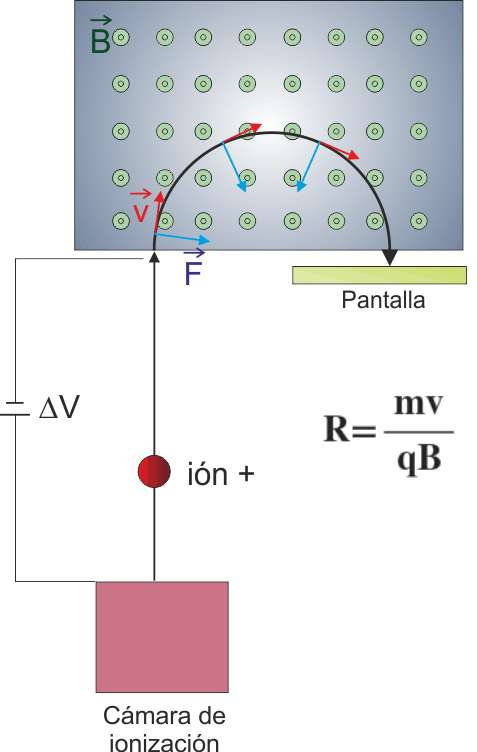 |
|
| Imagen de Juancarcole en Wikimedia Commons. CC |