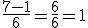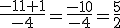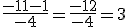2.1. Puntos de corte con el eje "x"
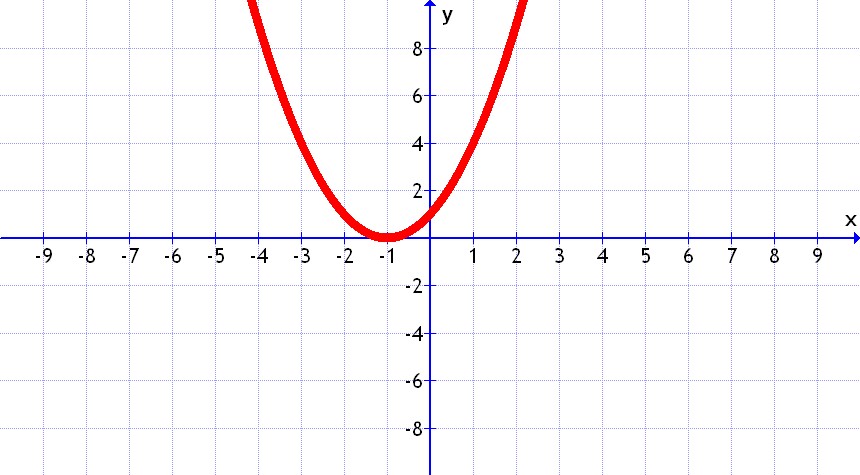
Se trata de encontrar los puntos en que la parábola corta con el eje "x" conociendo su ecuación. Además, esto nos va a servir de repaso para resolver ecuaciones de 2º grado ¿te acuerdas? las explicamos en el tema 3 de la unidad 1, en el segundo apartado del tema.
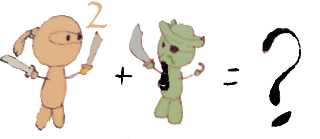
Como has visto en el ejercicio anterior la coordenada "y" en estos puntos debe ser siempre 0. Y esto es lo que nos va a servir para encontrar los puntos dada la ecuación de la parábola.
Pero vayamos paso a paso con un ejemplo:
1º Partimos de una ecuación, por ejemplo y = 3x2 -7x + 4
2º En los puntos en los que esta función corta al eje "x" la y = 0 y por tanto nuestro problema se reduce a resolver la siguiente ecuación:
3x2 - 7x + 4 = 0
3º Para eso aplicamos la fórmula de la ecuación de segundo grado. ¿Recuerdas el tema 3 de la unidad 1? Se hacía así:
Una ecuación de segundo grado se expresa de la forma ax2 + bx + c = 0, donde a ≠ 0. Esta ecuación se resuelve con la fórmula:
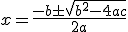
En nuestro caso sería: a=3 b=-7 c=4 (fíjate en nuestra ecuación, y = 3x2 -7x + 4, para obtener estos números)
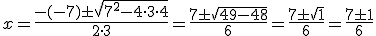
Ahora tenemos dos posibles soluciones:
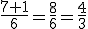
ó
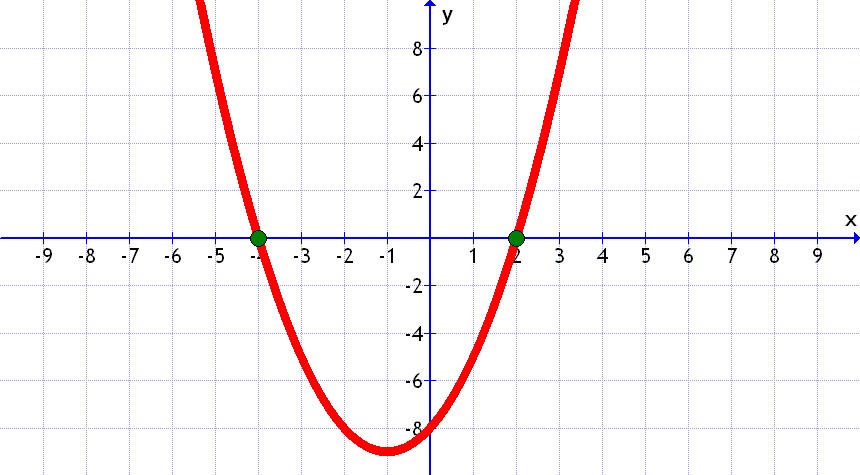
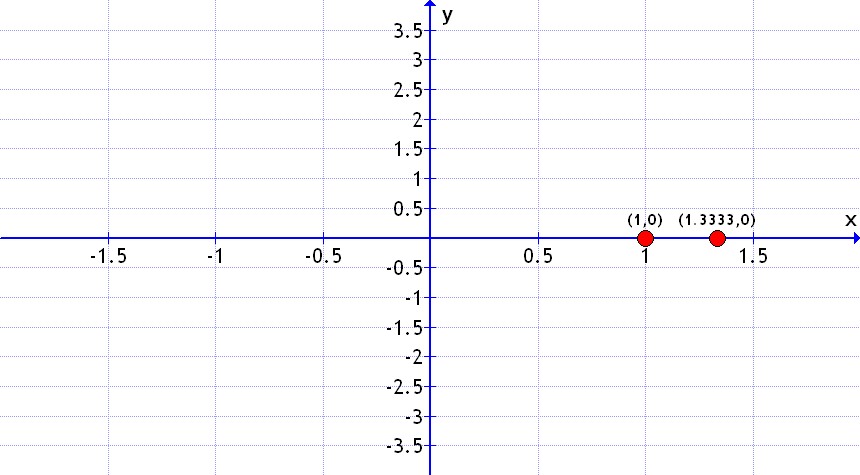
4º El resultado sería que la función corta al eje de abscisas (el eje de las "x") en x = 4/3 y en x = 1. O también podemos decirlo así:
Los puntos de corte con el eje de abscisas son (4/3 , 0) y (1 , 0) que es lo mismo.
AV - Actividad de Espacios en Blanco
Vamos a comprobar si te acuerdas de cómo de resolvían estas ecuaciones. Encuentra los puntos de corte con el eje "x" de la siguiente parábola:
f(x) = -2x2+ 11x - 15
Te recordamos que la ecuación de segundo grado puede tener:
- dos soluciones (como en los casos anteriores)
- una solución
- ninguna solución
Qué pasa en los dos últimos casos. Pues aquí tienes la respuesta con los siguientes ejemplos:
Actividad
Para encontrar los puntos de corte con el eje x de la parábola y = ax2 + bx + c hay que resolver la ecuación de segundo grado:
ax2 + bx + c = 0
aplicando la fórmula:
Puede suceder que:
| Corte en dos puntos (dos soluciones) |
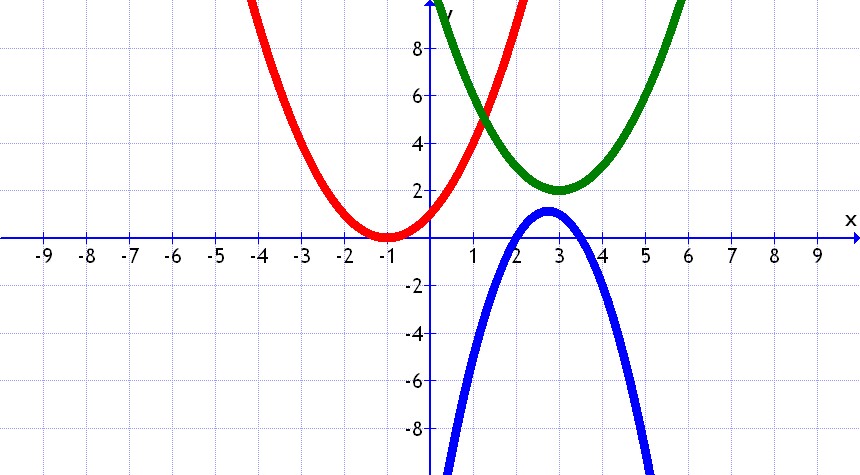 |
| Corte en un punto (una solución) |
|
| No corte en ningún punto (ninguna solución) |
AV - Reflexión
Encuentra los puntos de corte con el eje x de las siguientes funciones cuadráticas (o parábolas)
a. f(x) = 2x2 -5x + 2
b. f(x) = -x2 + 2x - 8
c. f(x) = -4x2 + 4x - 1