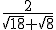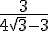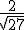1.2. Radicales. Operaciones
 |
| Fotografía en Flickr por Waka Jawaka bajo CC |
Hemos llegado a uno de los apartados más importantes del tema: la noción y el manejo de radicales.
Su importancia para nosotros no sólo se debe al papel que jugaron en el descubrimiento de los números irracionales, sino también por la frecuencia con que aparecen en la prueba que estamos preparando.
Ya hemos estudiado en el tema anterior operaciones como la suma, y la multiplicación, así como sus inversas, la resta y la división. Pero no podemos dejarnos en el tintero la potenciación. Observa el siguiente cuadro:
| Potenciación | Radicación |
|
Conocemos la base, 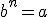 |
Conocemos la potencia, |
La radicación es una operación relacionada con la potenciación, y se representa utilizando el símbolo √ que proviene de la inicial de la palabra en latín, radix. En muchas ocasiones da como resultado un número irracional (recuerda que la raíz cuadrada de 2 fue posiblemente el primer número irracional conocido).
Actividad
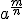 es un radical de índice
es un radical de índice 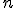 y radicando
y radicando 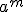 , y se denota por:
, y se denota por: 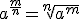
Actividad
Decimos que la raíz n-ésima de un número  es
es 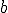 si cumple que
si cumple que 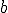 elevado a
elevado a 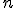 es
es  . Es decir:
. Es decir:
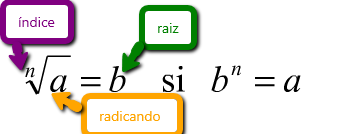
Imagen de elaboración propia
|
Pregunta de Elección Múltiple
Radicales equivalentes. Simplificar y operar con radicales.
En la siguiente presentación encontrarás un pequeño repaso a la teoría de radicales, cómo operar con ellos y muchos ejemplos. Pero no te preocupes, por si no es suficiente, algo más abajo entraremos en detalle de algunos de estos aspectos.
Además te enlazamos un pdf con un detallado resumen de la página 3con14. Para verlo haz clic en la siguiente imagen:
 |
En la anterior presentación has visto la teoría de radicales acompañada de ejemplos, pero debes tener en cuenta que las preguntas de este tipo en la prueba son frecuentes. Por eso es conveniente que aprendas a operar con ellos a la perfección y que mejor forma de conseguirlo, que viendo cómo se hace. A continuación te ofrecemos una serie de vídeos de juanmemol del canal de YouTube lasmatematicas.es. En dicho canal, puedes encontrar una sección de radicales que puede serte de gran ayuda, pero para que no te pierdas en la marabunta de vídeos (hay 52), te ofrecemos una pequeña muestra en la siguiente lista de reproducción de 6 vídeos:
Racionalización
Ya hemos visto en la presentación, que se llama así al proceso consistente en transformar expresiones en forma de cociente y con raíces en el denominador en otras expresiones en las que se han eliminado las raíces del denominador.
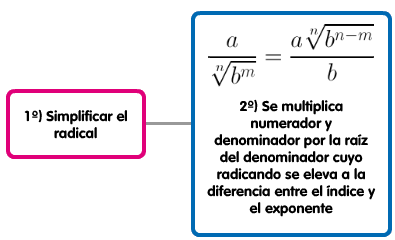
CASO I: El denominador es una única raíz
|
|
CASO II: El denominador es una suma o diferencia uno de cuyos operandos es una raíz cuadrada
 |
Caso de estudio
|
|
Curso 2010/2011
Racionalice las expresiones:
Caso de estudio
 |
Curso 2009/2010
Racionalice y simplifique la fracción: