2.2 Ecuación de las ondas armónicas

Como ya te habrás dado cuenta, las ondas tienen unas características un tanto singulares.

La existencia de una doble doble periodicidad, una con respecto al tiempo (periodo) y otra referida a la distancia con respecto al centro emisor (longitud de onda), las hace especiales. Luego para poder edificar un modelo adecuado desde una perspectiva matemática se debe encontrar una expresión adecuada que contemple esta doble periodicidad.

A la expresión anterior se le denominará ecuación de ondas y con la misma se pretende conocer el valor de la magnitud cuya propagación constituye la onda en cualquier punto del espacio que sea afectado o alterado por la misma y en cualquier instante después de que el foco emisor diera comienzo a la perturbación. Expuesto de otra forma, asignando a la variable “y” el valor de la perturbación, la ecuación nos servirá para valorar la modificación del medio a una distancia “x” concreta y en un tiempo “t” determinado desde el inicio de la emisión.

Para que no te hagas mucho lío, se parte de ciertas simplificaciones, con el fin de evitar un engorroso desarrollo físico, las mismas son:

1. Se supone puntual al foco emisor.
2. El movimiento armónico simple sirve de referencia para representar la perturbación del emisor, por lo que considero que la onda es armónica.
3. El foco en el instante inicial se hallaba en la posición de equilibrio, es decir, el ángulo de desfase del foco (δ) es nulo.
4. Se parte de la premisa que la onda es lineal y que el medio no absorbe ninguna energía de la onda. En tales condiciones, la amplitud de la onda no sufrirá ninguna variación en su valor y será, por tanto, constante.

Partiendo de lo anterior, el centro emisor responderá a un m.a.s. que comienza en el punto de equilibrio.

Un punto situado a cierta distancia “x” del centro emisor recibe los efectos de la perturbación transcurrido un cierto tiempo “t'” y, por tanto, tendrá el punto un cierto desfase, retardado en este caso, con respecto al centro emisor.

 

El desfase tomará, consecuentemente, un valor negativo y dependerá de la velocidad de propagación de la onda:

 

Otra forma de verlo es indicando que cualquier punto describe un movimiento armónico simple igual al que ejecutó el foco emisor un tiempo t=x/v antes, por lo tanto:  

Quedando la ecuación para cualquier valor del tiempo y la posición de las siguientes maneras:

 

 

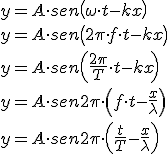
Tal y como está propuesto y el criterio de signo habitual, el punto “x” se sitúa a la derecha y delante de la variable de posición en la ecuación de onda se puede observar un signo negativo, consecuentemente, la presencia de ese signo indicará que la onda se desplaza hacia la derecha y si el signo fuera positivo, la onda se desplazaría hacia la izquierda. Pero esto debe ir en consonancia con el signo de la parte temporal y la función senoidal. Esa misma ecuación se puede expresar de otra forma empleando los conocimientos de la trigonometría:

Elaboración propia