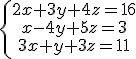2.3. Regla de Cramer
Gabriel Cramer nos mostró que los determinantes también nos pueden servir para resolver sistemas de ecuaciones, como vamos a ver a continuación.
 |
| Imagen en Wikimedia Commons. Dominio público. |
Importante
El sistema de ecuaciones
tiene como solución:
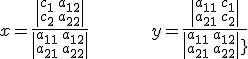
siempre que 
.
A esta forma de resolver sistemas de ecuaciones se le llama Regla de Cramer.
Si usamos la notación
Siendo D=El determinante de la matriz de coeficientes 
.
=El determinante de la matriz de los coeficientes en la cual se ha sustituido la primera columna (coeficientes de x) por los términos independientes (
).
=El determinante de la matriz de los coeficientes en la cual se ha sustituido la segunda columna (coeficientes de y) por los términos independientes ().
Podemos escribir la solución del sistema como
En los siguientes videos puedes ver ejemplos de resolución de sistemas de dos ecuaciones lineales por la regla de Cramer.
Caso práctico
Aplica la regla de Cramer para resolver el sistema 
.
Importante
En el caso de sistemas de tres ecuaciones lineales la regla de Cramer se aplica de la siguiente forma. El sistema siguiente.
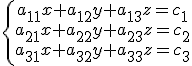
tiene como solución:
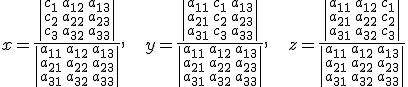
siempre que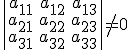 
.
Si usamos la notación
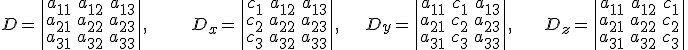
Siendo D=El determinante de la matriz de coeficientes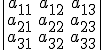 
.
=El determinante de la matriz de los coeficientes en la cual se ha sustituido la primera columna (coeficientes de x) por los términos independientes (
).
=El determinante de la matriz de los coeficientes en la cual se ha sustituido la segunda columna (coeficientes de y) por los términos independientes ().
Podemos escribir la solución del sistema como
En los siguientes videos puedes ver ejemplos de resolución de sistemas de tres ecuaciones lineales por la regla de Cramer.
Caso práctico
Resuelve el siguiente sistema de ecuaciones por la regla de Cramer.
