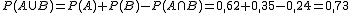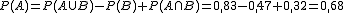Para cada suceso A, perteneciente a un espacio muestral E, se define la probabilidad de A, simbolizada por P(A), como un número que cumple los siguientes axiomas:
1. La probabilidad de cualquier suceso, es siempre mayor o igual que cero: P(A)≥0
2. La probabilidad del espacio muestral es 1: P(E)=1
3. Si tenemos un conjunto de sucesos incompatibles entre sí, entonces la probabilidad de la unión es igual a la suma de las probabilidades. En el caso conjuntos de dos y tres sucesos se expresaría así:
Si tenemos dos sucesos A, B incompatibles (A∩B=Ø) entonces se cumple que P(AUB)= P(A)+ P(B)
Si tenemos tres sucesos A, B, C, incompatibles dos a dos (A∩B=Ø, A∩C=Ø,B∩C=Ø) entonces se cumple que P(AUBUC)= P(A)+ P(B)+ P(C)
Por lo tanto la probabilidad de un suceso será un número comprendido entre 0 y 1 que mide la mayor o menor posibilidad de que ocurra dicho suceso. Cuanto más cerca de 1 es más probable que ocurra, cuanto más cerca de 0 más difícil.

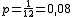 y
y 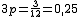 . Luego la P(2) = 0,25 y P(3) = 0,08.
. Luego la P(2) = 0,25 y P(3) = 0,08.