5.2. Circuitos en paralelo

Circuitos en paralelo

 

Para simplificar el trabajo con elementos conectados en paralelo vamos a introducir el concepto de admitancia.

Importante

Vamos a denominar admitancia al cociente entre la intensidad y la tensión y la denominaremos por "Y".

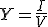
Y=\frac{I}{V}

Como puedes ver, la admitancia es simplemente la inversa de la impedancia:

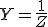
Y=\frac{1}{Z}

Pero seguro que te preguntas ¿Donde está la ventaja de trabajar con admitancias?

Pues bien, la admitancia equivalente, expresada en forma compleja, es igual a la suma de las admitancias de cada rama tal y como puedes ver a continuación:

Admitancia

Imagen 10.
Fuente: Elaboración propia creada con Paint.

De la figura anterior podemos ver fácilmente que:

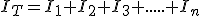
I_T=I_1+I_2+I_3+.....+I_n


Aplicando la Ley de Ohm:

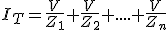
I_T= \frac{V}{Z_1} +\frac{V}{Z_2} +....+\frac{V}{Z_n}

Sacamos factor común a la tensión y nos queda que:


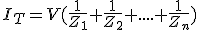
I_T= V (\frac{1}{Z_1} +\frac{1}{Z_2} +....+\frac{1}{Z_n})


Expresado utilizando el concepto de admitancia:

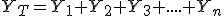
Y_T=Y_1+Y_2+Y_3+....+Y_n


Finalmente:

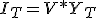
I_T=V*Y_T

Para que afiances el concepto vamos a resolver un ejercicio.

AV - Reflexión

Dado el circuito de la figura, calcula la admitancia, la impedancia y la intensidad generada por el alternador.

Ejercicio

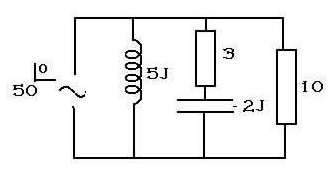
Imagen 12.
Fuente: Elaboración propia creada con Paint.