2.2. Funciones de probabilidad y distribución
Así es, las funciones nos informan.
Por ejemplo, en el caso de que conozcamos una variable aleatoria X, existen funciones asociadas a ella que nos dan información acerca de su comportamiento.
A continuación, vamos a ver dos de estas funciones: la función de probabilidad y la función de distribución.
Actividad
Si X es una variable aleatoria discreta, su distribución estará formada por los valores que puede tomar: x1, x2, x3, ..., xk y por las probabilidades de que ocurran cada uno de ellos: p1, p2, p3, ..., pk.
Estas cantidades p(X=xi) = pi, reciben el nombre de función de probabilidad y tienen las siguientes propiedades:
1. Son siempre positivas. (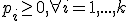 )
)
2. La suma de todas es igual a 1. (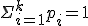 )
)
Veamos cómo se concreta en el juego de los caballos las definiciones del Importante anterior.
La siguiente tabla recoge la distribución de frecuencias y la probabilidad que tiene cada uno de los caballos de avanzar una posición en la carrera. A saber:
- xi representa cada uno de los posibles valores que puede tomar la variable X: "suma de los valores obtenidos al lanzar dos dados"
- ni es la frecuencia absoluta del valor xi.
- p(xi) es la probabilidad (frecuencia relativa) de que la variable X tome el valor xi
Ya hemos comentado que el resultado xi=1 es imposible de obtener al lanzar dos dados y sumarlos. Por tanto, el caballo número 1 no se moverá de la salida. Se ha incluído en la tabla para contemplar todos los números y ser coherentes con el juego.
| xi |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
ni |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 |
| p(xi) | 0/36 | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 5/36 | 1/36 |
El siguiente diagrama de barras muestra la distribución de probabilidad de la variable X. En el eje de abscisas (OX) se recogen las posibles sumas de los dos dados y en el eje de ordenadas (OY) la probabilidad (frecuencia relativa).
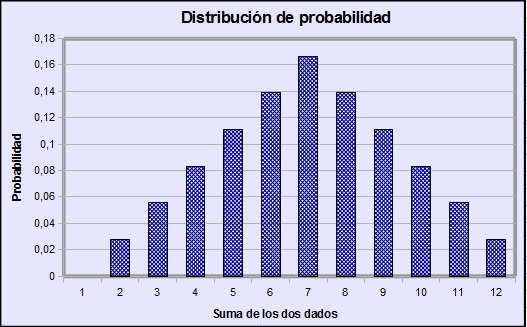 |
Ejemplo o ejercicio resuelto
 |
| 1/50pound coins are fake Imagen de xJasonrogersx, con licencia CC by 2.0 |
Consideremos la variable aleatoria X="número de caras obtenidas al lanzar tres veces una moneda"
(a) Indica los posibles valores X=xi que puede tomar la variable X.
(b) Determina el espacio muestral, E.
(c) Calcula la función de probabilidad, p(X=xi), de la variable X.
Actividad
Dada una variable aleatoria discreta (X) se define su función de distribución como:
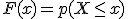
que asocia a cada número (x) la probabilidad acumulada hasta él.
Vamos a trabajar con la función de distribución de la variable X="número de caras obtenidas al lanzar tres veces una moneda"
AV - Pregunta Verdadero-Falso
p(X=x1)=p(X=0)=1/8=0,125
p(X=x2)=p(X=1)=3/8=0,375
p(X=x3)=p(X=2)=3/8=0,375
p(X=x4)=p(X=3)=1/8=0,125
Retroalimentación
Falso
p(X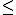 2) = p(X=0) + p(X=1) + p(X=2) = 0,125 + 0,375 + 0,375 = 0,875
2) = p(X=0) + p(X=1) + p(X=2) = 0,125 + 0,375 + 0,375 = 0,875
Retroalimentación
Verdadero
p(X<2) = p(X=0) + p(X=1) = 0,125 + 0,375 = 0,5