3. Fuerza sobre una espira

Imagen en Wikimedia Commons de Juancarcole
bajo licencia CC

Puede que, al leer el apartado anterior, te hayas preguntado, bueno ¿y qué?, ¿qué interés tiene conocer la formulita ?.

Vale, la idea de este apartado es que cambies de opinión o, mejor dicho, la concepción de lo que sigue es sentar las bases para que alteres tu parecer.

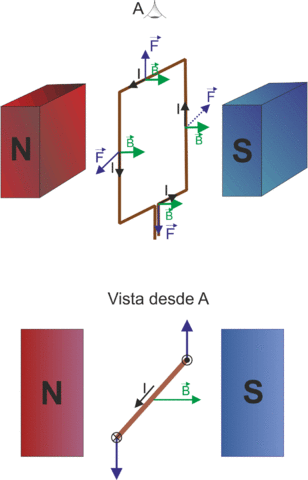
¿Cómo se va a hacer? Pues el quid de la cuestión está en imaginar una espira rectangular como la de la figura, por la que circula una corriente I, situada en un campo magnético constante B.

Todo lo que hay que hacer es aplicar la fórmula anterior a cada uno de los cuatro lados de la espira. Piénsalo y comprobarás lo siguiente:

Sobre los lados que se ha dibujado horizontales actúan fuerzas iguales y de sentido contrario. Ambas se anulan y no producen ningún efecto.
En cambio, sobre los lados dibujados verticalmente las dos fuerzas que actúan también son iguales y de sentido contrario pero, en este caso y como puedes comprobar en la parte inferior de la figura, ambas fuerzas no están alineadas y provocan un par que tiende a girar la espira.

Este giro de la espira es lo más interesante de todo esto que se está hablando. En general, se puede afirmar que, si se introduce una espira por la que circula una corriente en un campo magnético, la espira gira hasta situarse de forma perpendicular al campo.

Cuando la espira se coloca perpendicular al campo la espira está en equilibrio porque, tanto las fuerzas como los pares de fuerzas son cero.

Si quieres, puedes ampliar esta idea en el apartado siguiente.

Objetivos

En general, un objeto que tiene libertad para trasladarse o girar se encuentra en equilibrio cuando se cumplen dos condiciones:

Que la suma de las fuerzas que actúan sobre él sea cero (ΣF=0).
Que la suma de los momentos de las fuerzas respecto de cualquier punto sea cero (ΣM=0).

¿Qué es eso del momento de una fuerza y por qué no sabías nada de él hasta ahora?

El momento de una fuerza respecto de un punto se define como el producto vectorial , donde r es un vector que va desde el punto que sea hasta el punto de aplicación de la fuerza. Es importante que te des cuenta que el momento de una fuerza es una magnitud interesante en los movimientos de cuerpos que giran en torno a un punto como, por ejemplo, la espira analizada anteriormente. La razón por la que no sabías nada del momento es porque, hasta ahora, siempre has estudiado la física de una partícula, y una partícula no puede girar sobre sí misma. Pero, si se te viene a la cabeza el giro de la Tierra, basta con que pienses que está compuesta por muchas partículas.

Imagen en Wikimedia Commons de Juancarcole bajo licencia CC

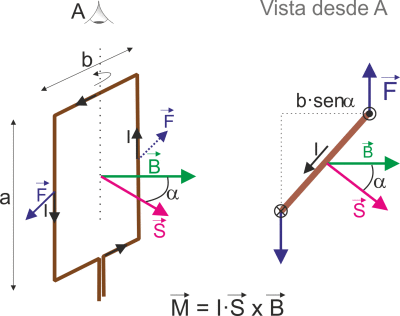
Fíjate ahora en la espira de la figura. El módulo de la fuerza magnética que actúa sobre cualquiera de los lados verticales, de longitud "a", se calcula de la siguiente forma:

y ambas fuerzas ejercen un momento sobre el punto medio del lado, que es el punto alrededor del cual viran o por donde pasa el eje de rotación o giro, que vale:

Sustituyendo el valor de F.

Esta expresión la podemos escribir de forma vectorial así:

donde es un vector perpendicular a la espira cuyo módulo coincide con su área, es decir: S=a·b