1. Fuerza de Lorentz
Usa imaginación y recréate en la configuración de una región del espacio donde existe un campo magnético B. En este apartado, se verá qué le pasa a una carga q cuando se encuentra en esa región. Para eso, lo más práctico es hacer la experiencia, ya sabes que la experiencia es el juez supremo de la física. Bien, pues resulta que, cuando se realiza ese experimento se observan varias cosas:
- Si la carga está en reposo, el campo magnético no actúa sobre ella, es decir, no se ejerce ninguna fuerza sobre ella.
- La carga se ve sometida a una fuerza sólo en el caso en que esté moviéndose a una cierta velocidad v. Esta fuerza es proporcional al valor de la carga q, es perpendicular a la velocidad v y depende de la dirección de movimiento (dirección de v), de tal forma que la fuerza es máxima cuando v es perpendicular a B, y es nula si v es paralela a B.
Recuerda que estos son resultados experimentales y, lo que son las matemáticas, resulta que este comportamiento de la carga en un campo magnético lo podemos representar matemáticamente por una fórmula muy simple, que recibe el nombre de Ley de Lorentz:
Pues bien, se va a proceder a hacer un análisis de la fórmula de Lorentz y verás que se ajusta a los resultados del experimento. Para empezar, al tratarse de un producto vectorial, el módulo de la fuerza se calcula así:
lo cual hace que:
- La fuerza es proporcional a "q" y a "v".
- Es perpendicular a v y a B. Su dirección la determina el signo de la carga y el sentido del producto vectorial vxB.
- Si v y B son perpendiculares, el sen(v,B)=1 y la fuerza es máxima:
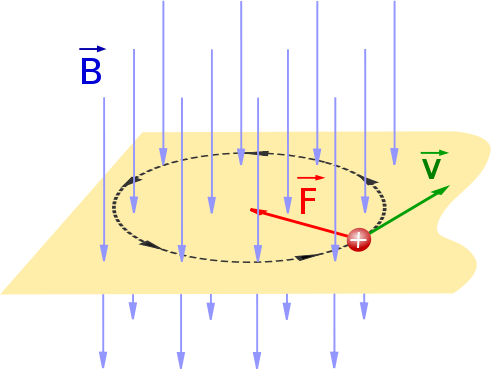
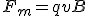. En cambio, si v y B son paralelos, el sen(v,B)=0 y la fuerza es nula. - Al ser la fuerza siempre perpendicular a "v", no producirá un cambio en el módulo de la velocidad, el efecto que produce sobre la carga es simplemente torcer su trayectoria de tal forma que, si la fuerza magnética es la única que actúa, se convierte en la fuerza centrípeta que obliga a la carga a describir una trayectoria circular. Un asunto interesante es calcular el radio de la trayectoria, para ello basta con igualar el módulo de la fuerza magnética con la expresión de la fuerza centrípeta (Fm=Fc).
 |
 |
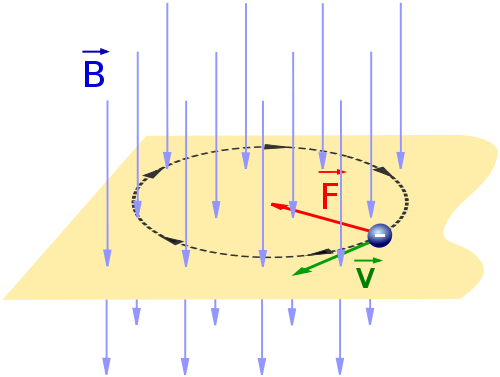| Imagen en Wikimedia Commons de Jfmelero bajo licencia CC | Imagen en Wikimedia Commons de Jfmelero bajo licencia CC |
Ya ves que hemos supuesto que "v" es perpendicular a "B", si no lo fuera, la trayectoria sería helicoidal, como puedes comprobar en el video a continuación
Conocimiento previo
Existe una regla que te puede venir bien para determinar la dirección de la fuerza magnética, se trata de la regla de la mano izquierda. Si colocas el dedo corazón en el sentido de v y el índice en el sentido de B, el pulgar marcará el sentido de F para una carga positiva. Si la carga es negativa será el sentido contrario.
Aquí no se han comido mucho el coco los científicos con el nombre le llaman la regla de la mano derecha, otra muy similar y con los mismos resultados es la regla del sacacorchos.
 |
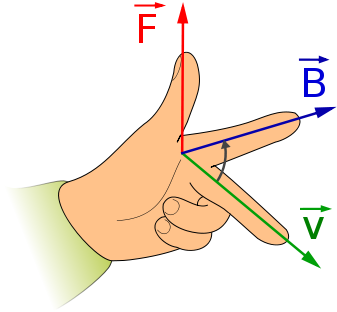| Imagen en Wikimedia Commons de Jfmelero bajo licencia CC |
Reflexión
A partir de la expresión matemática de la fuerza de Lorentz, ¿cuál crees que es el trabajo realizado por la fuerza magnética a lo largo de cualquier trayectoria?
Caso práctico
Dos partículas con cargas eléctricas, del mismo valor absoluto y diferente signo, se mueven con la misma velocidad, dirigida hacia la derecha y en el plano del folio. Ambas partículas penetran en un campo magnético de dirección perpendicular al folio y dirigido hacia abajo.
a) Analice con ayuda de un gráfico las trayectorias seguidas por las dos partículas.
b) Si la masa de una de ellas es doble que la de la otra (m1 = 2 m2 ) ¿Cuál gira más rápidamente?