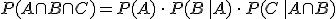2.3. Probabilidad condicionada
 |
| Imagen en Flickr por dsevilla bajo CC |
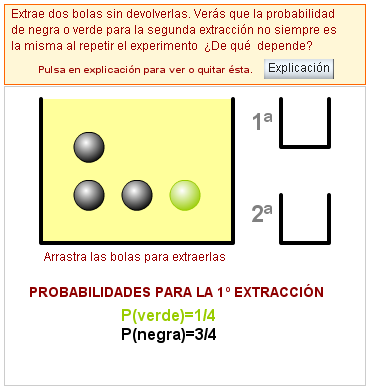
El efecto mariposa es un concepto que hace referencia a como unas condiciones iniciales diferentes, pueden variar un resultado. Ya a lo largo del tema hemos visto ejemplos de situaciones en que un resultado influye en los resultados siguientes (hacíamos varias extracciones de una urna sin reemplazamiento). Esto nos indica que hay veces que tenemos una información añadida que condicionará el resto del experimento.
Por ejemplo, si tenemos una urna con 2 bolas blancas y 3 bolas negras, podemos preguntarnos cuál es la probabilidad de extraer una bola negra, sabiendo que la primera fue blanca, es decir, tendremos que recorrer el árbol partiendo de una de las extracciones.
Esta información adicional, provoca que tengamos un nuevo espacio muestral de partida, que serían los casos en los que se cumple esa condición, es decir, tenemos nuestro efecto mariposa particular.
Actividad
En un experimento aleatorio dados dos sucesos A y B, se define el suceso “A condicionado a B” (A|B) como el suceso que ocurre cuando ocurre A, suponiendo que haya ocurrido B.
Se llama probabilidad condicionada del suceso A respecto del B y se denota P(A|B) al siguiente cociente:
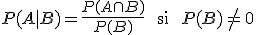
|
Caso de estudio
En un experimento se sabe que P(A)=0,4, P(B)=0,8 y P(A∪B)=0,85. Calcula las siguientes probabilidades:
a) P(A∩B)
b) P(A|B)
c) P(B|A)
Volvamos al caso de las urnas, y veamos el siguiente ejemplo:
Probabilidad y tablas de contingencia
Llevamos casi todo el tema organizando nuestra información en diagramas de árbol, pero también podemos recogerla mediante tablas de contingencia.
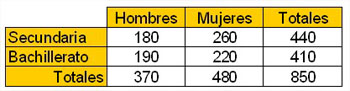
Por ejemplo, si vamos a hacer un análisis sobre los alumnos de un Instituto, en función del sexo y del nivel de estudios, los datos podemos ordenarlos:
|
¿Cómo calculamos probabilidades cuando nos organizamos de esta forma? Es muy sencillo como verás en la siguiente actividad, pero lo que debes tener presente es que necesitas saber los totales, es decir, los casos posibles.
Caso de estudio
Si elegimos una persona al azar, de los matriculados en esta enseñanza, ¿cuál es la probabilidad de ser?
a) Alumna de secundaria.
b) Alumno de bachillerato.
c) Si la persona que hemos elegido es de bachillerato, ¿cuál es ahora la probabilidad de que sea un alumno?
d) Si hemos elegido una persona al azar y sabemos que es mujer, ¿cuál es la probabilidad de que esté matriculada en secundaria?
Dependencia e independencia de sucesos
Si recuerdas en el apartado 1, estudiábamos alguna de las relaciones existentes entre dos sucesos, entre las que se encontraban la dependencia y la independencia. Pero aunque a priori, parezca sencillo determinar si dos sucesos son o no dependientes, en ocasiones no podemos deducirlo de la propia definición de estos sucesos.
En las extracciones con reemplazamiento cada extracción es independiente de las demás. Lo mismo ocurre en los lanzamientos de dados, monedas...
En las extracciones sin reemplazamiento el resultado obtenido en cada extracción condiciona las siguientes, de forma que cada experimento aleatorio simple es dependiente de los anteriores. Lo podrás comprobar pinchando en la siguiente imagen correspondiente al recurso de José Ireno Fernández Rubio, Emilio Pazo Núñez del proyecto Descartes:
Captura de pantalla del Proyecto Descartes
Actividad
Dos sucesos A y B son dependientes si la realización de A condiciona la probabilidad de B.
Si dos sucesos son dependientes: P(A ∩ B) = P(A|B) · P(B)
Dos sucesos A y B son independientes si la realización de A no condiciona la probabilidad de B.
Si dos sucesos A y B son independientes P(A) = P(A|B), es decir, la realización del suceso B no influye en la probabilidad de A, y la fórmula anterior queda como P(A ∩ B) = P(A) · P(B)
Pregunta Verdadero-Falso
Retroalimentación
Falso
Sabemos que P(A∪B)= P(A) + P(B) − P(A∩B).
Despejamos: P(A∩B)= P(A) + P(B) − P(A∪B)= 0,4 + 0,8 − 0,85= 0,35
Por otro lado P(A) · P(B)= 0,4 · 0,8 = 0,32.
Como P(A ∩ B) ≠ P(A) · P(B), A y B son dependientes.
Retroalimentación
Verdadero
Sabemos que P(A∪B)= P(A) + P(B) − P(A∩B).
Despejamos: P(A∩B)= P(A) + P(B) − P(A∪B)= 0,5 + 0,7 − 0,85= 0,35.
Por otro lado P(A) · P(B)= 0,5 · 0,7 = 0,35.
Como P(A ∩ B) = P(A) · P(B), A y B son independientes.
Quizás hayas reparado que en muchos de los ejemplos utilizados en este apartado, hemos trabajado con experimentos compuestos, los que ya abordamos en el apartado anterior. Pero si te paras a pensar, no llegamos a formalizar la idea mediante una fórmula.
Pues bien, ¡ya estamos en disposición de hacerlo! Si queremos hallar la probabilidad de que ocurran varios sucesos dependientes a la vez, hay que calcular la probabilidad del primer suceso, multiplicarlos por la probabilidad de que ocurra el segundo suceso, supuesto que ha ocurrido el primero, por la probabilidad de que ocurra el tercer suceso suponiendo que han ocurrido los dos primeros, y así sucesivamente. Para tres sucesos correspondería con la expresión: