2.2. Probabilidades más complejas

Probabilidad de operaciones con sucesos

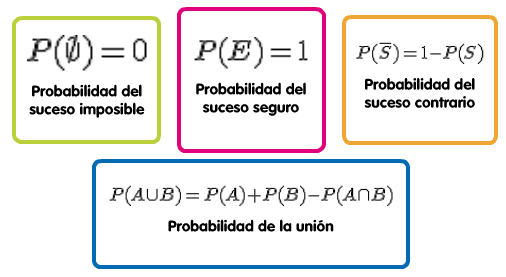
Después del apartado anterior, ya somos capaces de calcular probabilidades de sucesos fáciles, pero ya viste en el apartado 1.3 que los sucesos se podían operar y es verdad que a veces lo que queremos que suceda es una operación entre dos o más sucesos.

Imagen de elaboración propia

Recordar estas fórmulas es relativamente sencillo, sobre todo si las racionalizamos:

¿Por qué P(Ø)=0?

Ya vimos que por definición cuando la probabilidad estaba más cercana a 0, más improbable era que ocurriera. Por lo tanto, si es exactamente 0, no cabe duda que es un suceso que nunca llegará a ocurrir.

¿Por qué P(E)=1?

Es el mismo razonamiento que el suceso imposible. Si estamos ante algo seguro, tenemos la certeza de que ocurrirá por lo tanto, la probabilidad es 1.

¿Por qué P(AUB)=P(A)+P(B)-P(A∩B)?

Está claro que entre A y B forman la unión, pero si te fijas al tomar esa unión hay una parte que las estamos contando dos veces que es la parte que tienen en común A y B, es decir, su intersección.

¿Por qué ?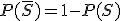

Porque entre S y su complementario forman el suceso seguro, y ambos son incompatibles por lo que si aplicamos la fórmula de la unión, obtenemos que .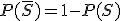

En el siguiente vídeo, podemos ver ejemplos y algo de teoría relacionada con la probabilidad de la unión de dos sucesos:

Probabilidad de experimentos compuestos

Ya hemos calculado probabilidades de sucesos más complejos como el de la unión, pero, ¿qué ocurre cuando es el experimento más complejo?

Te recordamos que un experimento compuesto es aquel en el que cada prueba equivale a la realización conjunta de varias pruebas simples, ya sea simultánea o sucesivamente. La probabilidad de un suceso de un experimento compuesto se calcula a partir de las probabilidades de los sucesos simples que lo forman.

Para calcular la probabilidad de un suceso de un experimento compuesto se pueden usar varios métodos. Una de estos métodos consiste en usar los diagramas en árbol. En el diagrama, en cada paso, vamos escribiendo las probabilidades de los experimentos simples que componen nuestro experimento compuesto.

Se observa el camino de las ramas que nos conducen a la solución. El producto de las probabilidades de las ramas de dicho camino será la probabilidad del suceso solución.

A continuación un vídeo de cómo enfrentarnos a este tipo de problemas, pero recuerda lo que vimos en el apartado 1, podemos trabajar con reemplazamiento o sin reemplazamiento: