2.1. Probabilidad de un suceso
 |
| Imagen en Flickr de mtraker bajo CC |
Definición clásica de probabilidad. Regla de Laplace
Imagina por un momento que sueles entrenar un equipo de fútbol juvenil. En el partido de este sábado acaban de pitar un penalti a favor de tu equipo y tienes que decidir quién lo tira y quieres elegir al que tenga más posibilidades de marcarlo. Tienes dos jugadores especialistas en lanzamientos de pena máxima, uno ha lanzado este año 12 penaltis y ha marcado 8, el otro ha lanzado 8 y ha conseguido 6 goles. ¿A quién elegirías?
En este apartado vamos a ver como asignarle a un suceso aleatorio una cantidad que mida lo probable o improbable de que ocurra ese suceso.
Actividad
Podemos definir la probabilidad de un suceso de una forma intuitiva (puedes ver una definición más formal en los apéndices), como un número comprendido entre 0 y 1 que mide la mayor o menor posibilidad de que ocurra dicho suceso. Cuanto más cerca de 1 es más probable que ocurra, cuanto más cerca de 0 más difícil.
 |
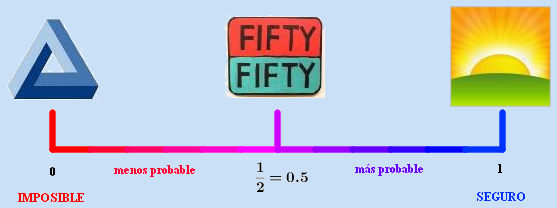| Imagen de elaboración propia |
Si estamos pensando en cuál de los dos jugadores elegir, quizás sea buena idea tener en cuenta la proporción de aciertos al lanzar el penalti. En el primer jugador sería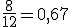 
y en el segundo sería 
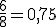, es decir, elegiríamos al segundo.
Pero, ¿qué ocurriría si el segundo jugador está saliendo de una lesión? Quizás, ahora esa proporción no sea del todo fiable a la hora de decantarme por uno o por otro.
Pongamos otro ejemplo.
Siempre que se oyen cuentos sobre gente que hace trampas en el juego, se habla de cartas marcadas, monedas o dados trucados, ruletas manipuladas y siempre en la línea de conseguir que los resultados que se esperan que tengan determinada probabilidad, se vean alterados.
Sin embargo, en este apartado no vamos a estudiar esos experimentos, sino que vamos a estudiar aquellos en los que todos los resultados tienen la misma oportunidad de suceder.
Importante
Por ejemplo, en una moneda no trucada, los sucesos "salir cara" y "salir cruz" tienen las mismas posibilidades de ocurrir. De la misma manera, en una baraja normal de cartas, si extraemos una al azar, cualquiera de las cartas tiene la misma posibilidad de salir.
Si estamos ante este caso, podemos recurrir a la definición clásica de probabilidad:
Importante
En un experimento con resultados equiprobables, la probabilidad de un suceso es el cociente entre el número de resultados favorables al suceso partido por el número de resultados posibles del experimento, es decir, el número de sucesos elementales. Este resultado se conoce como Regla de Laplace.
|
Esta definición teórica de probabilidad es útil en los experimentos aleatorios de tipo finito, cuando es posible obtener el número de casos favorables y el número de casos posibles y estos son igualmente probables.
Por ejemplo, vamos a trabajar el siguiente experimento: se lanza un dado dos veces y se suman los resultados. Vamos a calcular la probabilidad de que la suma sea 3, 12 y 7 puntos. El espacio muestral de este experimento serían todos los posibles resultados de sumar las puntuaciones de dos dados, es decir:
E = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
Pero, claro, no es igual de probable obtener de suma 12, cosa que solo puedo conseguir si me salen dos seis, que conseguir sumar 4.
Por lo tanto, para aplicar la regla de Laplace tengo que escribir TODOS los sucesos posibles, uno a uno, y todas las posibilidades que pueden suceder.
Lo organizamos en esta tabla:
| Suceso | Casos favorables |
Número de formas diferentes de conseguir el suceso
|
Probabilidad |
| {2} | (1,1) | 1 | 1/36 |
| {3} | (1,2), (2,1) |
2 | 2/36 |
| {4} |
(1,3), (3,1), (2,2) |
3 | 3/36 |
| {5} |
(1,4), (4,1), (2,3), (3,2) |
4 | 4/36 |
| {6} | (1,5), (5,1), (2,4), (4,2), (3,3) |
5 | 5/36 |
| {7} |
(1,6), (6,1), (2,5), (5,2), (3,4), (4,3) |
6 | 6/36 |
| {8} | (2,6), (6,2), (3,5), (5,3), (4,4) |
5 |
5/36 |
| {9} | (3,6), (6,3), (4,5), (5,4) | 4 | 4/36 |
| {10} | (4,6), (6,4), (5,5) |
3 | 3/36 |
| {11} | (5,6), (6,5) |
2 | 2/36 |
| {12} |
(6,6) |
1 | 1/36 |
De forma que la probabilidad de obtener de suma 3 sería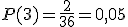 
La probabilidad de que la suma de los dados sea 12 sería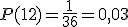 
La probabilidad de que la suma de los dados sea 7 sería 
Caso de estudio
 |
Curso 2009/2010
Se lanzan simultáneamente dos dados cuyas caras están numeradas del 1 al 6. ¿Cuál es la probabilidad de que la suma de las dos caras sea 12?
Caso de estudio
Tenemos un dado con 20 caras numeradas del 1 al 20 (cuya figura geométrica es el polígono regular llamado icosaedro), lo lanzamos y nos fijamos en qué número obtenemos. Queremos saber que probabilidad hay de obtener un número que sea:
- Múltiplo de 5.
- Mayor que 12.
- Mayor que 4 y menor que 12.
Importante
Existen otras definiciones de probabilidad, más generales:
- En una de ellas se toma como medida de la probabilidad de un suceso la frecuencia relativa con la que este aparece, ya que cuando va aumentando el número de veces que realizamos un experimento, la frecuencia relativa de cada resultado se va situando cada vez más alrededor de un determinado número que se mantiene constante cuando el número de lanzamientos es muy grande. Esa cantidad a la que tiende la frecuencia relativa coincide con la probabilidad del suceso.
- En otra se define la probabilidad como una función que cumple unos axiomas.
Ambas definiciones puedes encontrarlas con más detalle en el apéndice, incluso trabajaremos con la primera en el tema siguiente.