1.3. Operaciones con sucesos
Operaciones con sucesos
Cuando uno, en su tierna infancia, comienza a adentrarse en el apasionante mundo de las matemáticas, comienza con las cosas más simples: reconocer los números, contar, ordenar... y llega un momento en que se comienza a operar con esos números. A partir de ahí lo que hacemos es ampliar el número de operaciones que vamos conociendo y aplicando. Podemos pensar que solo podemos operar con números, pero vamos a ver en este apartado que también es posible operar con otros elementos, en nuestro caso con sucesos.
Ahora vamos a ver las dos operaciones fundamentales con sucesos y verás que quizás te recuerden cosas conocidas. ¿Recuerdas cuando calculábamos el m.c.d. y el m.c.m. de varios números?, en el primero escogíamos solo los factores comunes y en el segundo tomábamos los valores comunes y los no comunes, lógicamente sin repetir los comunes. Pues algo parecido veremos a continuación.
Importante
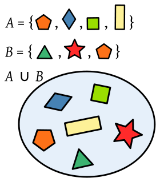
La unión de los sucesos A y B (AUB) es el suceso que tiene lugar cuando ocurre A o B, es decir, es el suceso que contiene exactamente los elementos de A y los elementos de B.
|
|
| Imagen en Wikimedia Commons de kismalac bajo CC |
Imagen en Wikimedia Commons de kismalac bajo CC |
IMPORTANTE: AUB se lee “A o B”, es decir, cuando nos encontremos en una actividad o problema, siempre que nos pregunten por A o B, nos están preguntando por la unión de dos sucesos.
Importante
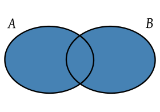
La intersección de sucesos A y B (A∩B) es el suceso que tiene lugar cuando ocurren simultáneamente A y B, es decir, es el suceso que contiene exactamente los elementos que pertenecen a la vez a A y a B.
 |
 |
| Imagen en Wikimedia Commons de kismalac bajo CC |
Imagen en Wikimedia Commons de kismalac bajo CC |
IMPORTANTE: A∩B se lee "A y B", es decir, cuando nos encontremos en un problema o actividad, siempre que nos pregunten por A y B, nos están preguntando por la intersección de los dos sucesos.
Caso de estudio
Si estamos ante el experimento aleatorio lanzar un dado, su espacio muestral asociado es E={1, 2, 3, 4, 5, 6}. Si definimos A="obtener número par", es decir, A={2, 4, 6} y B="obtener múltiplo de 3", es decir, B={3, 6}.
Determina los sucesos AUB y A∩B.
Importante
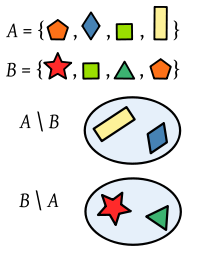
La diferencia de sucesos (A − B o A\B), es el suceso que tiene lugar cuando ocurre A y no B, es decir, está formado por los elementos de A que no son de B.
 |
 |
 |
|
IMPORTANTE: Observa en las imágenes que no es igual A-B que B-A.
Importante
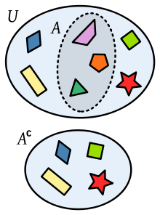
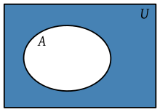
El suceso complementario (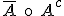
) de A tiene lugar cuando no ocurre A, es decir, está formado por todos aquellos elementos del espacio muestral que no están en A.
|
|
| Imagen en Wikimedia Commons de kismalac bajo CC |
Imagen en Wikimedia Commons de kismalac bajo CC |
IMPORTANTE: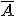 
se lee no A, es decir, cuando en un problema o actividad nos pregunten por la no ocurrencia de A, nos están preguntando por su complementario.
Además si te fijas A y 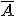guardan una relación de sucesos contrarios.
Caso de estudio
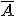y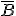 
.
Caso de estudio
Unos amigos se apuestan una cena, mediante una partida de dados. El experimento consistía en lanzar un dado y anotar el resultado, y los sucesos eran los siguientes:
A = "Salir un número impar" (ganaba Gonzalo)
B = "Salir un número primo" (ganaba Blanca)
C = "Salir un divisor de 6" (ganaba M.ª José)
D = "Salir un múltiplo de 4" (ganaba la amiga de M.ª José)
a) ¿Cuáles son los elementos del suceso donde ganan Gonzalo o Blanca?
b) ¿Cuáles son los elementos del suceso donde ganan M.ª José o su amiga?
c) ¿Cuáles son los elementos del suceso donde ganan Gonzalo y Blanca?
d) ¿Cuáles son los elementos del suceso donde ganan M.ª José y su amiga?
e) ¿Cuáles son los elementos del suceso donde gana Gonzalo y no gana Blanca?
f) ¿Cuáles son los elementos del suceso donde gana Blanca y no gana M.ª José?
Propiedades de las operaciones con sucesos
En la actividad resuelta anterior, A-B también podíamos expresarlo como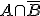 
, pues nos preguntaban por los elementos de A y los elementos que no estaban en B.
Esto nos indica que podemos encontrarnos con propiedades de las operaciones con sucesos (al igual que pasaba con los números) que nos ayuden a expresar lo mismo de una forma a priori más sencilla.
Como son muchas propiedades (asociativa de la unión y la intersección, conmutativa, distributiva...), te recomendamos el siguiente enlace donde todas vienen explicadas con mucho detalle. Sin embargo, debes prestar especial atención a las siguientes, las conocidas como "leyes de Morgan":
 |
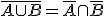Lo que no está en A o en B, dicho de otra forma lo que no está en A y no está en B |
 |
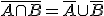Lo que no está en A y en B, dicho de otra forma lo que no está en A o no está en B |
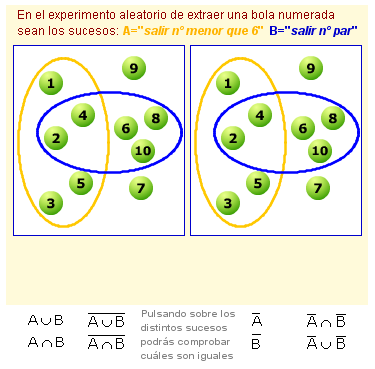
Si haces clic en la siguiente imagen descubrirás un applet María José García Cebrian del proyecto EDAD que seguro que te ayuda a entender algo mejor estas propiedades manipulando los sucesos A y B:
Por último, juanmemol en un vídeo de youtube nos resume estos dos últimos apartados, es decir, nos hablará de sucesos y de operaciones con sucesos: